Flow Induced Symmetry Breaking in a Conceptual Polarity Model

Abstract

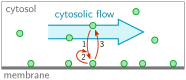
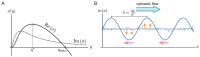
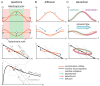
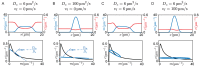
Important cellular processes, such as cell motility and cell division, are coordinated by cell polarity, which is determined by the non-uniform distribution of certain proteins. Such protein patterns form via an interplay of protein reactions and protein transport. Since Turing's seminal work, the formation of protein patterns resulting from the interplay between reactions and diffusive transport has been widely studied. Over the last few years, increasing evidence shows that also advective transport, resulting from cytosolic and cortical flows, is present in many cells. However, it remains unclear how and whether these flows contribute to protein-pattern formation. To address this question, we use a minimal model that conserves the total protein mass to characterize the effects of cytosolic flow on pattern formation. Combining a linear stability analysis with numerical simulations, we find that membrane-bound protein patterns propagate against the direction of cytoplasmic flow with a speed that is maximal for intermediate flow speed. We show that the mechanism underlying this pattern propagation relies on a higher protein influx on the upstream side of the pattern compared to the downstream side. Furthermore, we find that cytosolic flow can change the membrane pattern qualitatively from a peak pattern to a mesa pattern. Finally, our study shows that a non-uniform flow profile can induce pattern formation by triggering a regional lateral instability.

Keywords: cytoplasmic flow; pattern formation; phase-space analysis; symmetry breaking.

Figure 1

One-dimensional two-component system with cytosolic flow into the positive x-direction. The reaction kinetics include (1) attachment, (2) self-recruitment, and (3) enzyme-driven detachment.

Figure 2

(A) Sketch of real (solid) and imaginary (dotted) part of a typical dispersion relation with a band $[0,q_{\max }]$ of unstable modes. (B) The initial dynamics of a spatially homogeneous state with a small random perturbation (blue thin line). The direction of cytosolic flow is indicated by a blue arrow. The typical wavelength ($\lambda$) of the initial pattern is determined by the fastest growing mode $q^{*}$ and the phase velocity is determined by the value of the imaginary part of dispersion relation at the fastest growing mode ($v_{\mathrm{phase}}=-\mathrm{Im}\sigma \left(q^{*}\right)/q^{*}$). The growth of the pattern is indicated by orange arrows, while the traveling direction is indicated by pink arrows.

Figure 3

Sketch of the initial dynamics of an laterally unstable spatially homogeneous steady state. The role of reactions (A), diffusion (B), and advection (C) for a mass-redistribution instability are presented for the membrane (top) and cytosolic (middle) concentration profiles and in phase space (bottom). (A) A small perturbation of the spatially homogeneous membrane concentration (orange dashed lines in top panel) leads to a spatially varying local total density $n\left(x\right)$, with a larger total density at the maximum of the membrane profile (open circle) and a smaller total density at the minimum (open star). These local variations in total density lead to attachment zones (green region) and detachment zones (red region). The reactive flow, indicated by the red and green arrows, points along the reactive subspace (gray lines) in phase space towards the shifted local equilibria (black circles). These reactive flows lead to the solid orange density profiles after a small amount of time. (B) Faster diffusion in the cytosol compared to the membrane (indicated by the large and small blue arrows in the middle and top panel, respectively), lead to net mass transport from the detachment zone to the attachment zone. Again, dashed and solid lines indicate the state before and after a short time interval of diffusive transport. (C) Cytosolic flow shifts the cytosolic concentration with respect to the membrane concentration (orange dashed to orange solid lines), increasing the cytosolic concentration on the upstream side of the pattern and decreasing the cytosolic concentration on the downstream side. In phase space, the trajectory of this density profile forms a ‘loop’.

Figure 4

Pattern dynamics far from the spatially homogeneous steady state. (A) Time evolution of the membrane-bound protein concentration. At time $t_0=240 \mathrm{s}$ a constant cytosolic flow with velocity $v_{\mathrm{f}}=20 \mathsf{\mu }\mathrm{m}/\mathrm{s}$ towards the right is switched on (cf. Movie 3). (B) Relation between the peak speed ($v_{\mathrm{p}}$) and flow speed ($v_{\mathrm{f}}$). Results from finite element simulations (black open squares) are compared to the phase velocity of the mode $q_{\max }$ obtained from linear stability analysis (green solid line) and to an approximation (orange open circles) of the area enclosed by the density distribution trajectory in phase space (area enclosed by the ‘loop’ in D). (The domain size, $L=10 \mathsf{\mu }\mathrm{m}$, is chosen large enough compared to the peak width such that boundary effects are negligible.) (C) A schematic of the phase portrait corresponding to the pattern in D. The density distribution in the absence of flow is embedded in the flux-balance subspace (FBS) (blue straight line). In the presence of flow, the density distribution trajectory forms a ‘loop’ in phase space. The upstream and downstream side of the pattern are highlighted in cyan and magenta, respectively. Red and green arrows indicate the direction of the reactive flow in the attachment and detachment zones, respectively. At intersection points of the density distribution with the nullcline ($c_{\mathrm{L}}$ and $c_{\mathrm{R}}$) the system is at its local reactive equilibrium. (D) Sketch of the membrane (orange solid line, top) and cytosolic (orange dashed line, bottom) concentration profiles for a stationary pattern in the absence of cytosolic flow. Flow shifts the cytosol profile downstream (orange solid line, bottom).

Figure 5

Demonstration of the transition from a mesa pattern to a peak pattern. Each panel shows a snapshot from finite element simulations in steady state. Top concentration profiles in real space; bottom: corresponding trajectory (blue solid line) in phase space. (A) Mesa pattern in the case of slow cytosol diffusion and no flow. The two plateaus (blue dots) and the inflection point (gray dot) of the pattern correspond to the intersection points of the FBS (blue dashed line) with the reactive nullcline (black line). (B) For fast cytosol diffusion, the third intersection point between FBS and nullcline lies at much higher membrane concentration such that it no longer limits the pattern amplitude. Therefore, a peak forms whose amplitude is limited by the total protein mass in the system. (C) Slow flow only slightly deforms the mesa pattern, compare to (A). Fast cytosolic flow leads to formation of a peak pattern (D), similarly to fast diffusion. Parameters: $\overline{n}=7 \mathsf{\mu }{\mathrm{m}}^{-1},D_m=0.1 \mathsf{\mu }{\mathrm{m}}^2/\mathrm{s}$, and $L=20 \mathsf{\mu }\mathrm{m}$.

Figure 6

Flow-driven protein mass accumulation can induce pattern formation by triggering a regional lateral instability. (A) Top: quadratic flow velocity profile: $v_f\left(x\right)/v_{\max }=1-4{\left(x/L-1/2\right)}^2$. Bottom: illustration of the total density profiles at different time points starting from a homogeneous steady state (i) to the final pattern (iv); see Movie 5. Mass redistribution due to the non-uniform flow velocity drives mass towards the right hand side of the system, as indicated by the blue arrows. The range of total densities shaded in orange indicates the laterally unstable regime determined by linear stability analysis. Once the total density reaches this regime locally, a regional lateral instability is triggered resulting in the self-organized formation of a peak (orange arrow). (B) Sketch of the phase space representation corresponding to the profiles shown in A. Note that the concentrations are slaved to the reactive nullcline (black line) until the regional lateral instability is triggered. (C) Schematic representation of the state space of concentration patterns in a case where both the homogeneous steady state and a stationary polarity pattern are stable. Thin trajectories indicate the dynamics in the absence of flow and the pattern’s basin of attraction is shaded in orange. The thick trajectory connecting both steady states shows the flow-induced dynamics, corresponding to the sequence of states (i)–(iv) shown in A and B.