On some factors determining the pressure drop across tracheal tubes during high-frequency percussive ventilation: a flow-independent model

Abstract

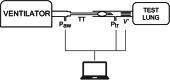
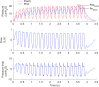
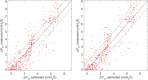
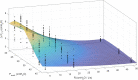
To provide an in vitro estimation of the pressure drop across tracheal tubes (ΔP_TT) in the face of given pulsatile frequencies and peak pressures (P_work) delivered by a high-frequency percussive ventilator (HFPV) applied to a lung model. Tracheal tubes (TT) 6.5, 7.5 and 8.0 were connected to a test lung simulating the respiratory system resistive (R = 5, 20, 50 cmH₂O/L/s) and elastic (C = 10, 20, and 50 mL/cmH₂O) loads. The model was ventilated by HFPV with a pulse inspiratory peak pressure (work pressure P_work) augmented in 5-cmH₂O steps from 20 to 45 cmH₂O, yielding 6 diverse airflows. The percussive frequency (f) was set to 300, 500 and 700 cycles/min, respectively. Pressure (Paw and Ptr) and flow (V') measurements were performed for all 162 possible combinations of loads, frequencies, and work pressures for each TT size, thus yielding 486 determinations. For each respiratory cycle ΔP_TT was calculated by subtracting each peak Ptr from its corresponding peak Paw. A non-linear model was constructed to assess the relationships between single parameters. Performance of the produced model was measured in terms of root mean square error (RMSE) and the coefficient of determination (r²). ΔP_TT was predicted by P_work (exponential Gaussian relationship), resistance (quadratic and linear terms), frequency (quadratic and linear terms) and tube diameter (linear term), but not by compliance. RMSE of the model on the testing dataset was 1.17 cmH₂O, r² was 0.79 and estimation error was lower than 1 cmH₂O in 68% of cases. As a result, even without a flow value, the physician would be able to evaluate ΔP_TT pressure. If the present results of our bench study could be clinically confirmed, the use of a nonconventional ventilatory strategy as HFPV, would be safer and easier.

Keywords: Biomedical modeling; Biomedical signal processing; High-frequency percussive ventilation; Respiratory mechanics; Tracheal tubes.

Fig. 1

Schematic diagram of experimental setup. Paw, airway pressure at the tube inlet; TT tracheal tube, Ptr distal tube pressure; V’ airflow

Fig. 2

From top to bottom: Pressures (Paw and Ptr, tube inlet and distal tube pressures, respectively), flow and pressure drop tracings during a single respiratory cycle. Circles indicate peak pressures during end-inspiratory plateau phase ΔP_TT = Paw_peak − Ptr_peak; P_work = 20 cmH₂O, f  = 300 cycles/min, R = 5 cmH₂O/L/s, C = 20 mL/cmH₂O, tube diameter 7.5 mm

Fig. 3

Comparison between calculated and experimental ΔP_TT for all 486 points (training set—left panel; testing set—right panel). Identity line; dashed lines represent ± 1 cmH₂O errors

Fig. 4

Relationship between peak pressure drop across the tracheal tube (ΔP_TT) and peak airway work pressure (P_work) and resistive load (R). All calculated 486 data points are presented. The grid surface describes the exponential Gaussian relationship and the quadratic model behavior expressed by the first term (0.0037 × R² – 0.35 × R + 8.63) × e^{−(Pwork−26.21)/14.47} of model reported in Eq. 1. The points dispersion around the grid is the expression of frequency and tube diameter variation considered by the final part of Eq. 1 (– 0.026 × f ² + 0.54 × f ) – 0.34 × TTD and the estimation error

Fig. 5

Work pressure (P_work) against measured peak flow (V’). From top to bottom the mechanical loads are R = 0, 5, 20, 50, ∞, respectively; C = 10 mL/cmH₂O; f = 500 cycles/min, tube diameter 7.5 mm. The lines represent the best fitting condition in each case