Three-dimensional US for Quantification of Volumetric Blood Flow: Multisite Multisystem Results from within the Quantitative Imaging Biomarkers Alliance
- PMID: 32602826
- PMCID: PMC7457950
- DOI: 10.1148/radiol.2020191332
Three-dimensional US for Quantification of Volumetric Blood Flow: Multisite Multisystem Results from within the Quantitative Imaging Biomarkers Alliance
Abstract
Background Quantitative blood flow (QBF) measurements that use pulsed-wave US rely on difficult-to-meet conditions. Imaging biomarkers need to be quantitative and user and machine independent. Surrogate markers (eg, resistive index) fail to quantify actual volumetric flow. Standardization is possible, but relies on collaboration between users, manufacturers, and the U.S. Food and Drug Administration. Purpose To evaluate a Quantitative Imaging Biomarkers Alliance-supported, user- and machine-independent US method for quantitatively measuring QBF. Materials and Methods In this prospective study (March 2017 to March 2019), three different clinical US scanners were used to benchmark QBF in a calibrated flow phantom at three different laboratories each. Testing conditions involved changes in flow rate (1-12 mL/sec), imaging depth (2.5-7 cm), color flow gain (0%-100%), and flow past a stenosis. Each condition was performed under constant and pulsatile flow at 60 beats per minute, thus yielding eight distinct testing conditions. QBF was computed from three-dimensional color flow velocity, power, and scan geometry by using Gauss theorem. Statistical analysis was performed between systems and between laboratories. Systems and laboratories were anonymized when reporting results. Results For systems 1, 2, and 3, flow rate for constant and pulsatile flow was measured, respectively, with biases of 3.5% and 24.9%, 3.0% and 2.1%, and -22.1% and -10.9%. Coefficients of variation were 6.9% and 7.7%, 3.3% and 8.2%, and 9.6% and 17.3%, respectively. For changes in imaging depth, biases were 3.7% and 27.2%, -2.0% and -0.9%, and -22.8% and -5.9%, respectively. Respective coefficients of variation were 10.0% and 9.2%, 4.6% and 6.9%, and 10.1% and 11.6%. For changes in color flow gain, biases after filling the lumen with color pixels were 6.3% and 18.5%, 8.5% and 9.0%, and 16.6% and 6.2%, respectively. Respective coefficients of variation were 10.8% and 4.3%, 7.3% and 6.7%, and 6.7% and 5.3%. Poststenotic flow biases were 1.8% and 31.2%, 5.7% and -3.1%, and -18.3% and -18.2%, respectively. Conclusion Interlaboratory bias and variation of US-derived quantitative blood flow indicated its potential to become a clinical biomarker for the blood supply to end organs. © RSNA, 2020 Online supplemental material is available for this article. See also the editorial by Forsberg in this issue.
Figures



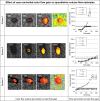

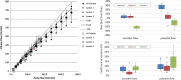
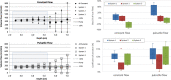
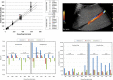
Comment in
-
Three-dimensional US Measurements of Blood Flow: One Step Closer to Clinical Practice.Radiology. 2020 Sep;296(3):671-672. doi: 10.1148/radiol.2020202419. Epub 2020 Jun 30. Radiology. 2020. PMID: 32609060 Free PMC article. No abstract available.
References
-
- Shung KK. Diagnostic ultrasound: imaging and blood flow measurements. 2nd ed. Boca Raton, Fla: CRC, 2015.
-
- Gill RW, Kossoff G, Warren PS, Garrett WJ. Umbilical venous flow in normal and complicated pregnancy. Ultrasound Med Biol 1984;10(3):349–363. - PubMed
-
- Gill RW. Measurement of blood flow by ultrasound: accuracy and sources of error. Ultrasound Med Biol 1985;11(4):625–641. - PubMed
-
- Holland CK, Clancy MJ, Taylor KJ, Alderman JL, Purushothaman K, McCauley TR. Volumetric flow estimation in vivo and in vitro using pulsed-Doppler ultrasound. Ultrasound Med Biol 1996;22(5):591–603. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

