Switching behaviour in vascular smooth muscle cell-matrix adhesion during oscillatory loading
- PMID: 32603668
- PMCID: PMC7384930
- DOI: 10.1016/j.jtbi.2020.110387
Switching behaviour in vascular smooth muscle cell-matrix adhesion during oscillatory loading
Abstract
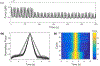
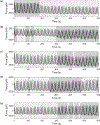
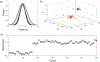
Integrins regulate mechanotransduction between smooth muscle cells (SMCs) and the extracellular matrix (ECM). SMCs resident in the walls of airways or blood vessels are continuously exposed to dynamic mechanical forces due to breathing or pulsatile blood flow. However, the resulting effects of these forces on integrin dynamics and associated cell-matrix adhesion are not well understood. Here we present experimental results from atomic force microscopy (AFM) experiments, designed to study the integrin response to external oscillatory loading of varying amplitudes applied to live aortic SMCs, together with theoretical results from a mathematical model. In the AFM experiments, a fibronectin-coated probe was used cyclically to indent and retract from the surface of the cell. We observed a transition between states of firm adhesion and of complete detachment as the amplitude of oscillatory loading increased, revealed by qualitative changes in the force timecourses. Interestingly, for some of the SMCs in the experiments, switching behaviour between the two adhesion states is observed during single timecourses at intermediate amplitudes. We obtain two qualitatively similar adhesion states in the mathematical model, where we simulate the cell, integrins and ECM as an evolving system of springs, incorporating local integrin binding dynamics. In the mathematical model, we observe a region of bistability where both the firm adhesion and detachment states can occur depending on the initial adhesion state. The differences are seen to be a result of mechanical cooperativity of integrins and cell deformation. Switching behaviour is a phenomenon associated with bistability in a stochastic system, and bistability in our deterministic mathematical model provides a potential physical explanation for the experimental results. Physiologically, bistability provides a means for transient mechanical stimuli to induce long-term changes in adhesion dynamics-and thereby the cells' ability to transmit force-and we propose further experiments for testing this hypothesis.
Keywords: Bistability; Dynamic loading; Integrins; Mechanotransduction.
Copyright © 2020 Elsevier Ltd. All rights reserved.
Conflict of interest statement
Declaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures
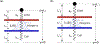
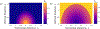


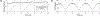
Similar articles
-
Effect of Loading History on Airway Smooth Muscle Cell-Matrix Adhesions.Biophys J. 2018 Jun 5;114(11):2679-2690. doi: 10.1016/j.bpj.2018.04.026. Biophys J. 2018. PMID: 29874617 Free PMC article.
-
Extracellular matrix-specific focal adhesions in vascular smooth muscle produce mechanically active adhesion sites.Am J Physiol Cell Physiol. 2008 Jul;295(1):C268-78. doi: 10.1152/ajpcell.00516.2007. Epub 2008 May 21. Am J Physiol Cell Physiol. 2008. PMID: 18495809 Free PMC article.
-
Characterisation of cellular adhesion reinforcement by multiple bond force spectroscopy in alveolar epithelial cells.Biol Cell. 2017 Jul;109(7):255-272. doi: 10.1111/boc.201600080. Epub 2017 Jun 23. Biol Cell. 2017. PMID: 28543271
-
Molecular mechanisms of mechanotransduction in integrin-mediated cell-matrix adhesion.Exp Cell Res. 2016 Nov 15;349(1):85-94. doi: 10.1016/j.yexcr.2016.10.001. Epub 2016 Oct 6. Exp Cell Res. 2016. PMID: 27720950 Free PMC article. Review.
-
Membrane adhesion junctions regulate airway smooth muscle phenotype and function.Physiol Rev. 2023 Jul 1;103(3):2321-2347. doi: 10.1152/physrev.00020.2022. Epub 2023 Feb 16. Physiol Rev. 2023. PMID: 36796098 Free PMC article. Review.
Cited by
-
Cell biomechanics on muscle atrophy: from intricate mechanisms to therapeutic frontiers.Ann Med. 2025 Dec;57(1):2540598. doi: 10.1080/07853890.2025.2540598. Epub 2025 Aug 1. Ann Med. 2025. PMID: 40747836 Free PMC article. Review.
-
Engineering of the microenvironment to accelerate vascular regeneration.Trends Mol Med. 2023 Jan;29(1):35-47. doi: 10.1016/j.molmed.2022.10.005. Epub 2022 Nov 9. Trends Mol Med. 2023. PMID: 36371337 Free PMC article. Review.
References
-
- Arthur D, Vassilvitskii S, 2007. k-means++: The advantages of careful seeding, in: Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics. pp. 1027–1035.
-
- Binnig G, Quate CF, Gerber C, 1986. Atomic force microscope. Physical Review Letters 56, 930. - PubMed
-
- Chan CE, Odde DJ, 2008. Traction dynamics of filopodia on compliant substrates. Science 322, 1687–1691. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

