Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Jun 27;13(13):2886.
doi: 10.3390/ma13132886.

Prediction of Static Modulus and Compressive Strength of Concrete from Dynamic Modulus Associated with Wave Velocity and Resonance Frequency Using Machine Learning Techniques

Jong Yil Park  1 , Sung-Han Sim  2 , Young Geun Yoon  3 , Tae Keun Oh  3   4
Affiliations

Prediction of Static Modulus and Compressive Strength of Concrete from Dynamic Modulus Associated with Wave Velocity and Resonance Frequency Using Machine Learning Techniques

Jong Yil Park et al. Materials (Basel). .

Abstract

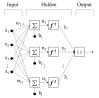
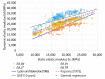
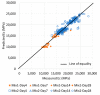
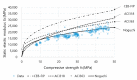
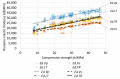
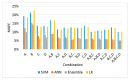
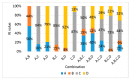
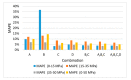
The static elastic modulus (Ec) and compressive strength (fc) are critical properties of concrete. When determining Ec and fc, concrete cores are collected and subjected to destructive tests. However, destructive tests require certain test permissions and large sample sizes. Hence, it is preferable to predict Ec using the dynamic elastic modulus (Ed), through nondestructive evaluations. A resonance frequency test performed according to ASTM C215-14 and a pressure wave (P-wave) measurement conducted according to ASTM C597M-16 are typically used to determine Ed. Recently, developments in transducers have enabled the measurement of a shear wave (S-wave) velocities in concrete. Although various equations have been proposed for estimating Ec and fc from Ed, their results deviate from experimental values. Thus, it is necessary to obtain a reliable Ed value for accurately predicting Ec and fc. In this study, Ed values were experimentally obtained from P-wave and S-wave velocities in the longitudinal and transverse modes; Ec and fc values were predicted using these Ed values through four machine learning (ML) methods: support vector machine, artificial neural networks, ensembles, and linear regression. Using ML, the prediction accuracy of Ec and fc was improved by 2.5-5% and 7-9%, respectively, compared with the accuracy obtained using classical or normal-regression equations. By combining ML methods, the accuracy of the predicted Ec and fc was improved by 0.5% and 1.5%, respectively, compared with the optimal single variable results.

Keywords: P-wave; S-wave; compressive strength; concrete; dynamic elastic modulus; machine learning; nondestructive method; resonance frequency test; static elastic modulus.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Experimental setup for determining static elastic modulus and compressive strength of concrete specimens.
Figure 2
Figure 2
Methods for measuring (a) ultrasonic pulse velocity using a P-wave transducer (MK 954) and (b) ultrasonic shear-wave velocity using an S-wave transducer (ACS T1802).
Figure 3
Figure 3
Resonance frequency test for (a) longitudinal mode and (b) transverse mode.
Figure 4
Figure 4
Procedure of support vector regression from an input sample.
Figure 5
Figure 5
Procedure of an artificial neural network from an input sample.
Figure 6
Figure 6
Procedure of an ensemble from an input sample.
Figure 7
Figure 7
Comparison of experimental and theoretical values for Ec and fc. (a) Static elastic modulus; (b) Compressive strength.
Figure 8
Figure 8
Relationship between Ec and Ed.
Figure 9
Figure 9
Comparison of individual Ed and Ec values.
Figure 10
Figure 10
Relationship between measured Ec and the ratio of predicted Ec to measured Ec using ML methods: (a) SVM; (b) ANN; (c) Ensemble; (d) LR.
Figure 11
Figure 11
Relationship between measured Ec (experimental values) and predicted Ec (theoretical values) by the ensemble.
Figure 12
Figure 12
Comparison of the relationships between Ec and fc.
Figure 13
Figure 13
Analysis of general regression for individual Ed and fc.
Figure 14
Figure 14
Comparison of MAPE for combinations using four ML methods.
Figure 15
Figure 15
Comparison of RI values using the ANN method.
Figure 16
Figure 16
Relationship between the measured Ec and the ratio of predicted fc to measured fc using the four ML methods. (a) SVM; (b) ANN; (c) Ensemble; (d) LR.
Figure 17
Figure 17
Relationship between measured fc (experimental values) and predicted fc (theoretical values) by the ensemble method.
Figure 18
Figure 18
MAPE values for each section of fc predicted using the ensemble method.
See this image and copyright information in PMC

References

    1. Mehta P.K., Monteiro P.J.M. Concrete-Microstructure, Properties, and Materials. 4th ed. McGraw-Hill Education; New York, NY, USA: 2013.
    1. ASTMC666/C666M-15 . Standard Test Method for Resistance of Concrete to Rapid Freezing and Thawing. ASTM International; West Conshohoken, PA, USA: 2015.
    1. Popovics J.S. ACI-CRC Final Report. American Concrete Institute; Farmington Hills, MI, USA: 2008. A study of static and dynamic modulus of elasticity of concrete.
    1. ASTM C597M-16 . Standard Test Method for Pulse Velocity through Concrete. ASTM International; West Conshohoken, PA, USA: 2016.
    1. ASTM C215-14 . Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens. ASTM International; West Conshohoken, PA, USA: 2016.

LinkOut - more resources