This is a preprint.
Practical considerations for measuring the effective reproductive number, R t
- PMID: 32607522
- PMCID: PMC7325187
- DOI: 10.1101/2020.06.18.20134858
Practical considerations for measuring the effective reproductive number, R t
Update in
-
Practical considerations for measuring the effective reproductive number, Rt.PLoS Comput Biol. 2020 Dec 10;16(12):e1008409. doi: 10.1371/journal.pcbi.1008409. eCollection 2020 Dec. PLoS Comput Biol. 2020. PMID: 33301457 Free PMC article.
Abstract
Estimation of the effective reproductive number, R t , is important for detecting changes in disease transmission over time. During the COVID-19 pandemic, policymakers and public health officials are using R t to assess the effectiveness of interventions and to inform policy. However, estimation of R t from available data presents several challenges, with critical implications for the interpretation of the course of the pandemic. The purpose of this document is to summarize these challenges, illustrate them with examples from synthetic data, and, where possible, make recommendations. For near real-time estimation of R t , we recommend the approach of Cori et al. (2013), which uses data from before time t and empirical estimates of the distribution of time between infections. Methods that require data from after time t, such as Wallinga and Teunis (2004), are conceptually and methodologically less suited for near real-time estimation, but may be appropriate for retrospective analyses of how individuals infected at different time points contributed to spread. We advise against using methods derived from Bettencourt and Ribeiro (2008), as the resulting R t estimates may be biased if the underlying structural assumptions are not met. Two key challenges common to all approaches are accurate specification of the generation interval and reconstruction of the time series of new infections from observations occurring long after the moment of transmission. Naive approaches for dealing with observation delays, such as subtracting delays sampled from a distribution, can introduce bias. We provide suggestions for how to mitigate this and other technical challenges and highlight open problems in R t estimation.
Figures
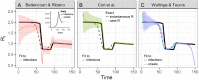


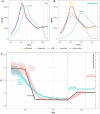
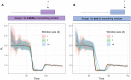
References
-
- Sciré J, Nadeau SA, Vaughan TG, Gavin B, Fuchs S, Sommer J, et al. Reproductive number of the COVID-19 epidemic in Switzerland with a focus on the Cantons of Basel-Stadt and Basel-Landschaft. Swiss Medical Weekly. 2020;150(19–20):w20271. - PubMed
-
- Flaxman S, Mishra S, Gandy A, et al. Estimating the number of infections and the impact of nonpharmaceutical interventions on COVID-19 in 11 European countries. Imperial College London; 2020. Available from: 10.25561/77731 - DOI
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
