Cochlea-inspired design of an acoustic rainbow sensor with a smoothly varying frequency response

Abstract

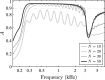
A number of physical arrangements for acoustic rainbow sensors have been suggested, where the aim is to separate different frequency components into different physical locations along the sensor. Although such spatial discrimination has been achieved with several designs of sensor, the resulting frequency responses at a given position along the sensor are generally not smoothly varying. In contrast, the cochlea provides an interesting natural example of a rainbow sensor, which has an exponential frequency distribution and whose response does vary smoothly with frequency. The design of a rainbow sensor is presented that has a number of discrete resonators and an exponential frequency distribution. We discuss the conditions for a smoothly varying frequency response in such a sensor, as part of a broader design strategy. It is shown that the damping within the resonators determines the trade-off between the frequency resolution and the number of elements required to achieve a smooth response. The connection is explained between this design and that of an effective acoustic absorber. The finite number of hair cells means that the cochlea itself can be thought of as being composed of discrete units and the conditions derived above are compared with those that are observed in the cochlea.

Fig. 1

Schematic of a cochlea-inspired acoustic rainbow sensor. (a) Longitudinal cross section along the mid-width plane of a system consisting of a square-cross-section duct of side $w_D$, with side branches consisting of Helmholtz resonators of varying dimensions. The neck radius, a, and length, $l_a$, are shown, along with the cavity volume, $V_H$. Each element of the system consists of a duct segment of length $l_D$ and a Helmholtz resonator. The length and width of each cavity are the same as those of the corresponding duct segment, and the height of each cavity is denoted by $h_H$. Formulas for the cross-sectional area of the duct, $S_D$, and of the neck, $S_H$, are shown, as well as for the volume of the cavity. The left and right ends of the system correspond to the base and the apex of the cochlea, respectively. (b) Circuit representation of an element of the system. $Z_1$ is the series impedance, consisting of the inertance of the duct, $L_D$, and $Z_2$ is the shunt impedance, consisting of the duct compliance, $C_D$, in parallel with an RLC branch representing the Helmholtz resonator, with resistance $R_H$, inertance $L_H$ and compliance $C_H$.

Fig. 2

Flow chart of the design procedure of the acoustic rainbow sensor.

Fig. 3

Wavenumber plots for the design example of an acoustic rainbow sensor. (a) Real and imaginary parts of the wavenumber plotted against the number of element, n, for a frequency of 1 kHz. (b) Real and imaginary parts of the wavenumber plotted against frequency for the 26th element. In (a), the vertical line corresponds to the the 26th element, whose resonance frequency, 985 Hz, is the closest to the input frequency. In (b), $f_1$ is the resonance frequency of the element used and $f_2$ is the corresponding cut-on frequency. The frequencies $f_1$ and $f_2$ form the limits of the stop band, which is shaded in grey.

Fig. 4

Pressure plots for the design example of an acoustic rainbow sensor. (a) Modulus of the pressure plotted against the number of element, n, for three different frequencies. (b) Modulus of the pressure plotted against frequency for three different elements. (c) Phase of the pressure plotted against n for three different frequencies. (d) Phase of the pressure plotted against frequency for three different elements. In (a) and (c), the coloured dashed vertical lines correspond to the elements whose resonance frequency is the closest to the respective input frequency; specifically, elements 12, 26 and 40 have resonance frequencies 1.97 kHz, 985 Hz and 492 Hz, respectively. In (b) and (d), the shaded areas correspond to the stop bands of the plot lines of similar colour. In all graphs, the solid lines correspond to the pressure in the resonators and the dotted lines to the pressure in the main duct.

Fig. 5

Simulations for different numbers of elements. (a), (c) and (e) Variation of the pressure in the resonators for different numbers of elements, N, at frequencies 500 Hz, 1 kHz and 2 kHz, respectively, plotted against the element number, n, normalised by the number of elements, N. (b), (d) and (f) Frequency response of the pressure in the resonators for different numbers of elements, N, at elements whose resonance frequency is the closest to 500 Hz, 1 kHz and 2 kHz, respectively; for $N=50$, these correspond to the 40th, the 26th and the 12th element.

Fig. 6

Absorption. Frequency variation of the absorption coefficient for different numbers of elements. The dashed horizontal line corresponds to a value of 0.9.