Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Jul 10;17(8):908-915.
doi: 10.1002/elsc.201700065. eCollection 2017 Aug.

Design of stable metabolic networks

Jimena Di Maggio  1 , Aníbal M Blanco  1 , J Alberto Bandoni  1 , Juan Carlos Díaz Ricci  2 , M Soledad Diaz  1
Affiliations

Design of stable metabolic networks

Jimena Di Maggio et al. Eng Life Sci. .

Abstract

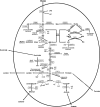
In this work, we propose eigenvalue optimization combined with Lyapunov theory concepts to ensure stability of the Embden-Meyerhof-Parnas pathway, the pentose-phosphate pathway, the phosphotransferase system and fermentation reactions of Escherichia coli. We address the design of a metabolic network for the maximization of different metabolite production rates. The first case study focuses on serine production, based on a model that consists of 18 differential equations corresponding to dynamic mass balances for extracellular glucose and intracellular metabolites, and thirty kinetic rate expressions. A second case study addresses the design problem to maximize ethanol production, based on a dynamic model that involves mass balances for 25 metabolites and 38 kinetic rate equations. The nonlinear optimization problem including stability constraints has been solved with reduced space Successive Quadratic Programming techniques. Numerical results provide useful insights on the stability properties of the studied kinetic models.

Keywords: Eigenvalue optimization; Metabolic networks; Non‐linear dynamic models; Optimal design; Stability.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Central carbon metabolism and fermentation pathways of E. coli.
Figure 2
Figure 2
Optimal concentrations for metabolic network designs with and without stability constraints for maximization of serine production.
Figure 3
Figure 3
Optimal fluxes distribution for serine production maximization at the reference steady state (⊡) and at the stable steady state.
Figure 4
Figure 4
Optimal concentrations for metabolic network designs with and without stability constraints for maximization of ethanol production.
Figure 5
Figure 5
Optimal fluxes distribution for ethanol production maximization at the reference steady state (⊡) and at the stable steady state.
See this image and copyright information in PMC

References

    1. Diaz Ricci, J. C. , Influence of phosphoenolpyruvate on the dynamic behavior of phosphofructokinase of Escherichia coli . J. Theor. Biol. 1996, 178, 145–150.
    1. Hatzimanikatis, V. , Bailey, J. , Studies on glycolysis.1. Multiple steady states in bacterial glycolysis. Chem. Eng. Sci. 1997, 52, 2579–2588.
    1. Haddad, W. , Chellaboina, V. , Stability and dissipativity theory for nonnegative dynamical systems: A unified analysis framework for biological and physiological systems. Nonlinear Analysis‐Real World Appl. 2005, 6, 33–65.
    1. Ivanov, O. , Schaft, A. , Weissing, F. , Steady states and stability in metabolic networks without regulation. J. Theor. Biol. 2016, 401, 78–93. - PubMed
    1. Theisen, M. K , Lafontaine Rivera, J. G. , Liao, J. C. , Stability of ensemble models predicts productivity of enzymatic systems. PLoS Comput. Biol. 2016, 12, e1004800 10.1371/journal.pcbi.1004800. - DOI - PMC - PubMed

LinkOut - more resources