The principles and methods behind EFSA's Guidance on Uncertainty Analysis in Scientific Assessment

Abstract

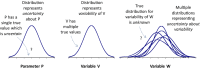
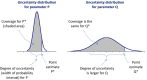
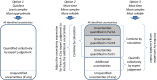
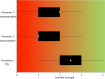
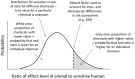
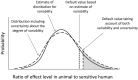
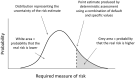
To meet the general requirement for transparency in EFSA's work, all its scientific assessments must consider uncertainty. Assessments must say clearly and unambiguously what sources of uncertainty have been identified and what is their impact on the assessment conclusion. This applies to all EFSA's areas, all types of scientific assessment and all types of uncertainty affecting assessment. This current Opinion describes the principles and methods supporting a concise Guidance Document on Uncertainty in EFSA's Scientific Assessment, published separately. These documents do not prescribe specific methods for uncertainty analysis but rather provide a flexible framework within which different methods may be selected, according to the needs of each assessment. Assessors should systematically identify sources of uncertainty, checking each part of their assessment to minimise the risk of overlooking important uncertainties. Uncertainty may be expressed qualitatively or quantitatively. It is neither necessary nor possible to quantify separately every source of uncertainty affecting an assessment. However, assessors should express in quantitative terms the combined effect of as many as possible of identified sources of uncertainty. The guidance describes practical approaches. Uncertainty analysis should be conducted in a flexible, iterative manner, starting at a level appropriate to the assessment and refining the analysis as far as is needed or possible within the time available. The methods and results of the uncertainty analysis should be reported fully and transparently. Every EFSA Panel and Unit applied the draft Guidance to at least one assessment in their work area during a trial period of one year. Experience gained in this period resulted in improved guidance. The Scientific Committee considers that uncertainty analysis will be unconditional for EFSA Panels and staff and must be embedded into scientific assessment in all areas of EFSA's work.

Keywords: guidance; principles; scientific assessment; uncertainty analysis.

Figure 1

Illustration of the distinction between uncertainty and variability (left and central graphs), and that both can affect the same quantity (right hand graph)

Figure 2

Illustration of the distinction between ‘coverage’ and ‘degree of uncertainty’ as measures of degree of conservatism. The distributions show uncertainty for two parameters P and Q. The point estimates P* and Q* have equal coverage (probability of lower values) but different degrees of uncertainty

Figure 3

Illustration of options for characterising overall uncertainty. See text for further explanation

Figure B.1

Confidence matrix used by IPCC (Mastrandrea et al., 2010). Confidence increases towards the top‐right corner as suggested by the increasing strength of shading. Generally, evidence is most robust when there are multiple, consistent independent lines of high‐quality evidence

Figure B.2

Example of matrix used for combining two ordinal scales representing uncertainty. In this example, the two input scales represent uncertainty in different parts of the uncertainty analysis (uncertainty about exposure to welfare hazards, and uncertainty about the probability of adverse effects given that exposure occurs) and their combination expresses the uncertainty of the assessment as a whole

Figure B.3

Strength of the information for parameter estimation in the melamine risk assessment. The diamond shows the median of scores of all seven experts on all four dimensions, the black box the interquartile range and the error bars the range of all scores. Colour shading ranges from green to reflect high parameter strength to red to reflect low parameter strength

Figure B.4

Strength and influence diagram for parameter uncertainty in the melamine risk assessment. The diamond shows the median of scores of all seven experts on all four dimensions for strength and the median score of all seven experts for influence. Colour shading ranges from green to reflect high parameter strength and low influence to red to reflect low parameter strength and high influence

Figure B.5

Scale used for assessing uncertainty in example evaluation (Table B.10)

Figure B.6

The process of expert knowledge elicitation (EFSA, 2014a)

Figure B.7

Confidence regions for distribution parameters for gamma distribution used to model variability of consumption by 1‐year‐old children

Figure B.8

Estimates of parameters of log‐normal distribution fitted to data sets obtained by resampling the body weight data. The red point shows the estimates for the original data

Figure B.9

Posterior distributions of parameters of log‐normal distribution for body weight of 1‐year‐old children. The left panel shows the probability density for σ_logbw,  the standard deviation of log bw. The panel on the right shows the conditional probability density for μ_logbw, the mean of log bw, given a value for the standard deviation σ_logbw

Figure B.10

Monte Carlo sample of 1,000 values representing posterior uncertainty about σ_logbw and μ_logbw, given the data

Figure B.11

Monte Carlo sample representing posterior uncertainty about parameters for the gamma distribution describing variability of consumption. The left panel shows uncertainty about the shape and rate parameters. The panel on the right shows uncertainty about the mean (kg/day) and coefficient of variation of the consumption distribution

Figure B.12

Distributions used to represent uncertainty about input parameters in worst‐case exposure assessment for children aged from 1 up to 2 years

Figure B.13

Uncertainty, calculated by MC, about worst‐case exposure for children aged from 1 up to 2 years

Figure B.14

Plot of estimated cumulative distribution of ratio of exposure to the TDI for melamine, for 1‐year‐olds consuming contaminated chocolate from China. Uncertainty about the cumulative distribution is indicated: the light grey band corresponds to 95% uncertainty range, and dark grey band corresponds to 50% uncertainty range

Figure B.15

Plot, as in Figure B.14 but with logarithmic scale for r, of cumulative distribution of ratio of exposure to the TDI for melamine, for 1‐year‐olds consuming contaminated chocolate from China. Uncertainty about the cumulative distribution is indicated: the light grey band corresponds to 95% uncertainty range, and dark grey band corresponds to 50% uncertainty range

Figure B.16

Graphical representation of the general concept for default assessment factors for inter‐ and intraspecies differences in toxicity

Figure B.17

Graphical representation of how uncertainty about the distribution for variability between chemicals can be taken into account when setting a default assessment factor

Figure B.18

Graphical illustration of treatment of uncertainty for a chemical‐specific adjustment factor for inter‐ or intraspecies differences in toxicokinetics or toxicodynamics

Figure B.19

Graphical illustration of assessing the combined conservatism of the output of a deterministic assessment, relative to a specified measure of risk. The distribution is not quantified by the deterministic assessment, so conservatism of the point estimate has to be assessed either by expert judgement, by probabilistic modelling, or by comparison with measured data on risk

Figure B.20

Examples of graphical methods for sensitivity analysis

Figure B.21

Results of break‐even sensitivity analysis

Figure B.22

Elementary effects of input factors in the melamine model on the risk ratio r, according to the method of Morris (160 samples). See text for explanation of red and blue lines

Figure B.23

Monte Carlo filtering for melamine example: pdf's of c and q producing favourable (r ≤ 0.1) or unfavourable (r > 0.1) results

Figure B.24

Model output uncertainty pdf for risk ratio r (x‐axis) (N = 5,120 samples)

Figure B.25

Sobo–Owen analysis of sensitivity of the 95th percentile of the risk‐ratio r to uncertainties about statistical parameters

Figure B.26

Uncertainty about the 95th percentile of the risk‐ratio r in four scenarios for the parameter σ_logc which is the standard deviation of log concentration. Three scenarios show the consequences of fixing the parameter at different percentiles of uncertainty and the fourth shows the consequence of using the full distribution of uncertainty for the parameter