Estimation of incubation period and generation time based on observed length-biased epidemic cohort with censoring for COVID-19 outbreak in China

Abstract

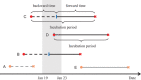
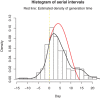
The incubation period and generation time are key characteristics in the analysis of infectious diseases. The commonly used contact-tracing-based estimation of incubation distribution is highly influenced by the individuals' judgment on the possible date of exposure, and might lead to significant errors. On the other hand, interval censoring-based methods are able to utilize a much larger set of traveling data but may encounter biased sampling problems. The distribution of generation time is usually approximated by observed serial intervals. However, it may result in a biased estimation of generation time, especially when the disease is infectious during incubation. In this paper, the theory from renewal process is partially adopted by considering the incubation period as the interarrival time, and the duration between departure from Wuhan and onset of symptoms as the mixture of forward time and interarrival time with censored intervals. In addition, a consistent estimator for the distribution of generation time based on incubation period and serial interval is proposed for incubation-infectious diseases. A real case application to the current outbreak of COVID-19 is implemented. We find that the incubation period has a median of 8.50 days (95% confidence interval [CI] [7.22; 9.15]). The basic reproduction number in the early phase of COVID-19 outbreak based on the proposed generation time estimation is estimated to be 2.96 (95% CI [2.15; 3.86]).

Keywords: deconvolution; interval censoring; mixture distribution; renewal process; serial interval.

FIGURE 1

Illustration of complete incubation period and forward time Note. Red circle: getting infected; blue column: departure from Wuhan; red cross: symptoms onset. The shaded area is the period during which our cohort sample departed from Wuhan. This figure shows five types of individuals. Only those who departed from Wuhan in the shaded area were collected in our cohort. (A) Symptoms onset in Wuhan, not in our cohort; (B and C) captured in our cohort with infection before departure; (D) captured in our cohort with infection at departure; (E) infection outside Wuhan, not in our cohort. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

FIGURE 2

Histogram of serial interval data and density of generation time in simulation Note. The expectation and variance of generation time and incubation period are listed in each subfigure. Black line: true density; cyan line: Gamma fit of S by deleting negative observations; red line: estimated density. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

FIGURE 3

COVID‐19 data analysis result Note. Upper: twice of log‐likelihood ratio, $2[{\max }_{\mathit{\theta },\pi }\ell (\mathit{\theta },\pi )-{\max }_{\mathit{\theta }}\ell (\mathit{\theta },\pi )]$, versus π. The dashed line is at 2.71, the 90% quantile of chi‐squared distribution with 1 degree of freedom. In fact, the horizontal ordinate of the crossover point is the 95% upper bound of π by likelihood ratio, since $0.5+0.5{\chi }^2(2.71,1)=0.95$ (mixed chi‐squared distribution), where ${\chi }^2(·,1)$ is the cdf of chi‐squared distribution with 1 degree of freedom. Lower: incubation estimation; red line: forward time fit; blue line: incubation period fit; black line: mixed observed time fit (covered by the red line). This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

FIGURE 4

Estimated generation time density (red line) using 71 observed serial intervals in COVID‐19 outbreak Note. The black line is the density of serial interval data. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.