Winter is coming: Pathogen emergence in seasonal environments

Abstract

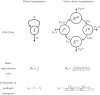
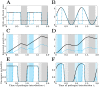
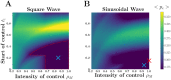
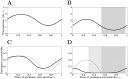
Many infectious diseases exhibit seasonal dynamics driven by periodic fluctuations of the environment. Predicting the risk of pathogen emergence at different points in time is key for the development of effective public health strategies. Here we study the impact of seasonality on the probability of emergence of directly transmitted pathogens under different epidemiological scenarios. We show that when the period of the fluctuation is large relative to the duration of the infection, the probability of emergence varies dramatically with the time at which the pathogen is introduced in the host population. In particular, we identify a new effect of seasonality (the winter is coming effect) where the probability of emergence is vanishingly small even though pathogen transmission is high. We use this theoretical framework to compare the impact of different preventive control strategies on the average probability of emergence. We show that, when pathogen eradication is not attainable, the optimal strategy is to act intensively in a narrow time interval. Interestingly, the optimal control strategy is not always the strategy minimizing R0, the basic reproduction ratio of the pathogen. This theoretical framework is extended to study the probability of emergence of vector borne diseases in seasonal environments and we show how it can be used to improve risk maps of Zika virus emergence.

Fig 1. Transmission mode and pathogen emergence without seasonality.

In a direct transmission model pathogen dynamics is driven by the birth rate λ and the death rate μ of a single infected compartment I. In a vector borne transmission model pathogen dynamics is driven by the birth rates and death rates of multiple compartments: exposed and infected humans (E^H, I^H), exposed and infected mosquito vectors (E^V, I^V). In the absence of seasonality (i.e. no temporal variation in birth and death rates) the basic reproduction ratio R₀ can be expressed as a ratio between birth and death rates. The probability of emergence p_e after the introduction of a single infected individual can also be expressed as a function of these birth and death rates. With vector borne transmission this probability of emergence depends on which infected host is introduced (Figure E in S1 Text). Here we give the probability of emergence after the introduction of a single human exposed to the pathogen, E^V, and where the index i refers to the four consecutive states of the pathogen life cycle (see sections 2 and 3 of S1 Text).

Fig 2. The winter is coming effect.

Pathogen birth rate (i.e. transmission rate) λ(t) is assumed to vary periodically following a square wave (A and B). During a portion 1 − γ of the year transmission is maximal (γ = 0.7 in this figure) and λ(t) = λ₀. In the final portion of the year λ(t) drops (low transmission season in gray). In A λ(t) varies between λ₀ = 2.5 and 1.5 and, in B λ(t) varies between λ₀ = 2.5 and 0. Pathogen death rate μ(t) (a function of recovery and death rates of the infected host) is assumed to be constant and equal to 1 in this figure. When the net growth rate of the pathogen remains positive in the low transmission season (λ(t) > μ(t), A, C and E) the probability of emergence of a pathogen introduced at time t₀ can be well approximated by Eq (6): $p_e\left(t_0\right)\simeq 1-\frac{\mu \left(t_0\right)}{\lambda \left(t_0\right)}$ (dashed line in E and F) if the duration of the infection is short relative to the period T of the fluctuation (E). In contrast, if the low transmission season is more severe (λ(t) < μ(t), B, D and F), the negative growth rate φ(t) of the pathogen population during this period creates a demographic trap and reduces the probability of emergence at the end of the high transmision season. This winter is coming effect is indicated with black arrow in (D) and with the light gray shading in (D) and (F). This effect is particularly pronounced when the period of the fluctuations of the environment is large relative to the duration of the infection (i.e., when T is large, F). When the period T of the fluctuation is small relative to the duration of the infection, the probability of emergence is well approximated by Eq (5): $p_e\simeq 1-\frac{1}{R_0}$ whatever the time of pathogen introduction (in A, R₀ = 2.2 and p_e ≃ 0.55; in B, R₀ = 1.75 and p_e ≃ 0.43).

Fig 3. Optimal Control for square wave (A, C and E) and sinusoidal birth rates (B, D and F).

In A and B we plot The pathogen birth rate before (black line) and after the optimal control (dashed blue line) which minimizes the mean emergence probability < p_e> (see also Fig 4). The square wave assumes that λ(t) = 3 1_(0<t<0.7). The sinusoidal wave assumes that λ(t) = 2(1 + sin(2πt)). As in Fig 2 the gray shadings refers to the low transmission season (gray) and the winter is coming effect (light gray). Similarly, we indicate the additional low transmission period induced by control (blue shading) and the additional winter is coming effect induced by control (light blue shading).

Fig 4. Mean probability of pathogen emergence for different control strategies with (A) square wave and (B) sinusoidal wave fluctuations.

We used the same scenarios as in Fig 3 and we fix the investment in control (cost of control C = ρ_M(t₂ − t₁) = 0.2). We explore how the intensity of control (ρ_M) and the timing of control (between t₁ and t₂) affect < p_e >, the mean probability of pathogen emergence (lighter shading refers to higher values of < p_e >). For the square wave scenario we identify a range of optimal strategies withing the dotted red curve where < p_e > is minimized. The optimal strategies used in Fig 3 are indicated with a blue cross for both the square wave (A) and the sinusoidal wave (B). The minimal and maximal value for < p_e > are: 0.166 − 0.366 (square wave) and 0.085 − 0.31 (sinusoidal wave). For the square wave (A), R₀ = 1.5 does not depend on the timing and the intensity of the control. For the sinusoidal wave (B), there is a single strategy minimizing R₀, namely R₀ = 1.28 for t₁ = 0.15 and ρ_M = 1.0, marked with a red cross in B. With the sinusoidal wave there is a single control strategy minimizing < p_e > for t₁ = 0.07 and ρ_M = 0.93 (blue cross in B).

Fig 5. Probability of Zika emergence across space and time.

The top figures (A and B) show the seasonal variations in λ_{I^V, E^H}, the transmission rate from humans to the vectors because of the fluctuations the density of vectors in two habitats (this illustrates the effect of space on Zika emergence): a minor variation in mean temperature, 29°C (A and C) versus 27°C (B and D), has a massive impact on transmission and, consequently, on pathogen emergence. In C and D we illustrate the effect of the time of introduction t₀ on Zika emergence. The dotted black line refers to the naive expectation for the probability of pathogen emergence at time t₀ if all the rates were constant and frozen at their t₀ values (see (7)). The gray shading in B and D refers to the low transmission season where the product of the transmission rates is lower than the product of death rates (see S1 Text). The exact probability of emergence p_e(t₀ T, T) is indicated as a solid black line. Higher seasonality (B and D) increases the discrepancy between the naive expectation and the exact value of the probability of pathogen emergence. This discrepancy is due to the winter is coming effect (light gray shading in D). Parameter values are given in table S1 A (model I) of section 3 of S1 Text.