Holography and Coherent Diffraction Imaging with Low-(30-250 eV) and High-(80-300 keV) Energy Electrons: History, Principles, and Recent Trends
- PMID: 32664297
- PMCID: PMC7412140
- DOI: 10.3390/ma13143089
Holography and Coherent Diffraction Imaging with Low-(30-250 eV) and High-(80-300 keV) Energy Electrons: History, Principles, and Recent Trends
Abstract
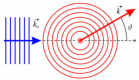
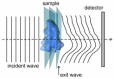
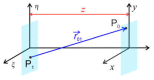
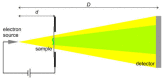
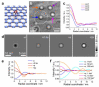
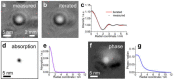
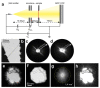
In this paper, we present the theoretical background to electron scattering in an atomic potential and the differences between low- and high-energy electrons interacting with matter. We discuss several interferometric techniques that can be realized with low- and high-energy electrons and which can be applied to the imaging of non-crystalline samples and individual macromolecules, including in-line holography, point projection microscopy, off-axis holography, and coherent diffraction imaging. The advantages of using low- and high-energy electrons for particular experiments are examined, and experimental schemes for holography and coherent diffraction imaging are compared.
Keywords: biomolecules; coherent diffraction imaging; diffraction; electron holography; holography; in-line holography; iterative phase retrieval.
Conflict of interest statement
The authors declare no conflict of interest.
Figures






















References
-
- Broglie L.D. Ph.D. Thesis. Sorbonne Université; Paris, France: 1924. Recherches sur la Théorie des Quanta.
-
- Davisson C., Germer L.H. The scattering of electrons by a single crystal of nickel. Nature. 1927;119:558–560. doi: 10.1038/119558a0. - DOI
-
- NIST . NIST Electron Elastic-Scattering Cross-Section Database. National Institute of Standards and Technology; Gaithersburg, MA, USA: 2000.
-
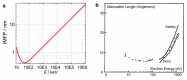
- Seah M.P., Dench W.A. Quantitative electron spectroscopy of surfaces: A standard data base for electron inelastic mean free paths in solids. Surf. Interface Anal. 1979;1:2–11. doi: 10.1002/sia.740010103. - DOI
-
- Spence J.C.H. STEM and shadow-imaging of biomolecules at 6 eV beam energy. Micron. 1997;28:101–116. doi: 10.1016/S0968-4328(97)00008-5. - DOI
Publication types
LinkOut - more resources
Full Text Sources

