Conditional permutation importance revisited

Abstract

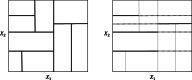
Background: Random forest based variable importance measures have become popular tools for assessing the contributions of the predictor variables in a fitted random forest. In this article we reconsider a frequently used variable importance measure, the Conditional Permutation Importance (CPI). We argue and illustrate that the CPI corresponds to a more partial quantification of variable importance and suggest several improvements in its methodology and implementation that enhance its practical value. In addition, we introduce the threshold value in the CPI algorithm as a parameter that can make the CPI more partial or more marginal.

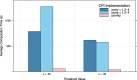
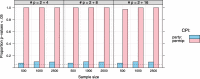
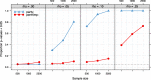
Results: By means of extensive simulations, where the original version of the CPI is used as the reference, we examine the impact of the proposed methodological improvements. The simulation results show how the improved CPI methodology increases the interpretability and stability of the computations. In addition, the newly proposed implementation decreases the computation times drastically and is more widely applicable. The improved CPI algorithm is made freely available as an add-on package to the open-source software R.

Conclusion: The proposed methodology and implementation of the CPI is computationally faster and leads to more stable results. It has a beneficial impact on practical research by making random forest analyses more interpretable.

Keywords: Conditional permutation importance; R; Random forest.

Fig. 1

Permutation scheme for the original PI (left) and for the CPI (right). In the permutation scheme of the original PI (left) the values of X_k are permuted against both Y and Z_(−k). In the permutation scheme of the CPI (right) the values of X_k are permuted against Y conditionally on the values of Z_(−k)

Fig. 2

Tree-growing (left) and conditional permutation (CPI; right) predictor space partitioning. In the tree-growing partitioning (left), only one split completely splits the predictor space, all the other splits are conditional on the previous split(s). In the partitioning that is used for permutation scheme in the CPI, where the predictor of interest is X_k=X₁ and $Z_{(-k)}^{\left(s\right)}=X_2$ (right), the splits with respect to X₂ are extended to completely split the predictor space (dashed lines) while the splits with respect to X₁ are ignored (gray lines)

Fig. 3

Computation speed: party vs. permimp implementation. Fifteen RFs (using ntree =1000 and mtry =10) were fit to a peptide-binding data set [5, 36]. The data set includes 310 observations of 105 predictors for a binary outcome. CPI according the old and the current party implementation as well as the permimp implementation were computed for two threshold values: s=.20 and s=.95. The average computation speed for the three implementations are given as respectively blue and red bars

Fig. 4

Non-linear dependencies: party vs. permimp implementation. Data sets were sampled with five, nine or seventeen uniformly distributed (min = -3, max = 3) predictors. An additional predictor was created by squaring one of the uniform predictors, so that all but two predictors were independent, and two showed a perfect quadratic relation. This resulted in two quadratically related predictors plus either four, eight or sixteen independent predictors. Sample size was either N=500,1000, or 2500, and either no, half or all the predictors had a linear impact on the continuous outcome variable. The dependence tests within the party and the permimp implementation (i.e., a χ²-test based on the tree-growing split points) were applied only to the two predictors with the perfect quadratic relation. The proportion of p-values lower than.05 within the party and permimp implementation are indicated in blue and pink respectively. The dashed line corresponds to a proportion of.05

Fig. 5

Sample size dependence: party vs. permimp implementation. Data sets were sampled with pairwise correlations of either ρ=.00,.05,.10, or.25 between 18 normally distributed predictors. Sample size was either N=500,1000, or 2500, and either no, half or all the predictors had a linear impact on the continuous outcome variable. The dependence tests within the party (correlation t-test) and the permimp implementation (χ²-test based on the tree-growing split points) were applied. The proportion of p-values lower than.05 within the party and permimp implementation are indicated in blue and pink respectively. The dashed line corresponds to a proportion of.05

Fig. 6

Stability of the CPI: party vs. permimp implementation. Data were generated according to a linear model with 12 uncorrelated normally distributed predictors, the regression coefficients were 5, 5, 2, 0, -5, -5, -2, 0, 0, 0, 0, and 0. In each of the 1000 replications 1000 observations were sampled, and a regression RF with 1000 trees was fit, after which the CPI was computed with a threshold value of s=0.5. The mean CPI (lines) as well as the region between the first and third quartile (shaded area) of the CPI distribution across the 1000 replications are depicted for every predictor, both for the party and the permimp implementation of the CPI, in blue and red, respectively. As a reference, the unconditional PI, which corresponds to the CPI with a threshold value of s=1 regardless of the implementation, is depicted in black. Because all predictors are independent, the PI and the CPI have demonstrate the same pattern