Magnetically Induced Carrier Distribution in a Composite Rod of Piezoelectric Semiconductors and Piezomagnetics
- PMID: 32668643
- PMCID: PMC7412448
- DOI: 10.3390/ma13143115
Magnetically Induced Carrier Distribution in a Composite Rod of Piezoelectric Semiconductors and Piezomagnetics
Abstract
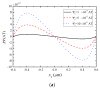
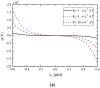
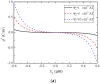
In this work, we study the behavior of a composite rod consisting of a piezoelectric semiconductor layer and two piezomagnetic layers under an applied axial magnetic field. Based on the phenomenological theories of piezoelectric semiconductors and piezomagnetics, a one-dimensional model is developed from which an analytical solution is obtained. The explicit expressions of the coupled fields and the numerical results show that an axially applied magnetic field produces extensional deformation through piezomagnetic coupling, the extension then produces polarization through piezoelectric coupling, and the polarization then causes the redistribution of mobile charges. Thus, the composite rod exhibits a coupling between the applied magnetic field and carrier distribution through combined piezomagnetic and piezoelectric effects. The results have potential applications in piezotronics when magnetic fields are relevant.
Keywords: applied magnetic field; carrier tuning; piezoelectric semiconductor; piezomagnetic.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

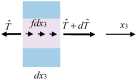







References
-
- Wang Z.L., Wu W.Z., Falconi C. Piezotronics and piezo-phototronics with third-generation semiconductors. MRS Bull. 2018;43:922–927. doi: 10.1557/mrs.2018.263. - DOI
-
- Zhang Y., Leng Y.S., Willatzen M., Huang B.L. Theory of piezotronics and piezo-phototronics. MRS Bull. 2018;43:928–935. doi: 10.1557/mrs.2018.297. - DOI
-
- Hu W.G., Kalantar-Zadeh K., Gupta K., Liu C.P. Piezotronic materials and large-scale piezotronics array devices. MRS Bull. 2018;43:936–940. doi: 10.1557/mrs.2018.292. - DOI
-
- Fröemling T., Yu R.M., Mintken M., Adelung R., Rödel J. Piezotronic sensors. MRS Bull. 2018;43:941–945. doi: 10.1557/mrs.2018.294. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

