A universal trade-off between growth and lag in fluctuating environments
- PMID: 32669712
- PMCID: PMC7442741
- DOI: 10.1038/s41586-020-2505-4
A universal trade-off between growth and lag in fluctuating environments
Abstract
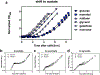
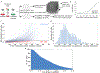
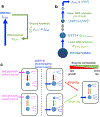
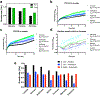
The rate of cell growth is crucial for bacterial fitness and drives the allocation of bacterial resources, affecting, for example, the expression levels of proteins dedicated to metabolism and biosynthesis1,2. It is unclear, however, what ultimately determines growth rates in different environmental conditions. Moreover, increasing evidence suggests that other objectives are also important3-7, such as the rate of physiological adaptation to changing environments8,9. A common challenge for cells is that these objectives cannot be independently optimized, and maximizing one often reduces another. Many such trade-offs have indeed been hypothesized on the basis of qualitative correlative studies8-11. Here we report a trade-off between steady-state growth rate and physiological adaptability in Escherichia coli, observed when a growing culture is abruptly shifted from a preferred carbon source such as glucose to fermentation products such as acetate. These metabolic transitions, common for enteric bacteria, are often accompanied by multi-hour lags before growth resumes. Metabolomic analysis reveals that long lags result from the depletion of key metabolites that follows the sudden reversal in the central carbon flux owing to the imposed nutrient shifts. A model of sequential flux limitation not only explains the observed trade-off between growth and adaptability, but also allows quantitative predictions regarding the universal occurrence of such tradeoffs, based on the opposing enzyme requirements of glycolysis versus gluconeogenesis. We validate these predictions experimentally for many different nutrient shifts in E. coli, as well as for other respiro-fermentative microorganisms, including Bacillus subtilis and Saccharomyces cerevisiae.
Conflict of interest statement
Ethics declarations
The authors declare no competing financial or non-financial interest.
Figures


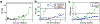



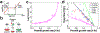


Comment in
-
Implications of initial physiological conditions for bacterial adaptation to changing environments.Mol Syst Biol. 2020 Sep;16(9):e9965. doi: 10.15252/msb.20209965. Mol Syst Biol. 2020. PMID: 32965749 Free PMC article.
References
-
- Scott M, Gunderson CW, Mateescu EM, Zhang Z & Hwa T Interdependence of cell growth and gene expression: origins and consequences. Science 330, 1099–102 (2010). - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

