A Path Toward Explainable AI and Autonomous Adaptive Intelligence: Deep Learning, Adaptive Resonance, and Models of Perception, Emotion, and Action
- PMID: 32670045
- PMCID: PMC7330174
- DOI: 10.3389/fnbot.2020.00036
A Path Toward Explainable AI and Autonomous Adaptive Intelligence: Deep Learning, Adaptive Resonance, and Models of Perception, Emotion, and Action
Abstract
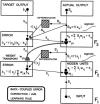
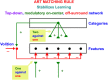
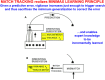
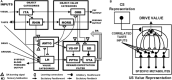
Biological neural network models whereby brains make minds help to understand autonomous adaptive intelligence. This article summarizes why the dynamics and emergent properties of such models for perception, cognition, emotion, and action are explainable, and thus amenable to being confidently implemented in large-scale applications. Key to their explainability is how these models combine fast activations, or short-term memory (STM) traces, and learned weights, or long-term memory (LTM) traces. Visual and auditory perceptual models have explainable conscious STM representations of visual surfaces and auditory streams in surface-shroud resonances and stream-shroud resonances, respectively. Deep Learning is often used to classify data. However, Deep Learning can experience catastrophic forgetting: At any stage of learning, an unpredictable part of its memory can collapse. Even if it makes some accurate classifications, they are not explainable and thus cannot be used with confidence. Deep Learning shares these problems with the back propagation algorithm, whose computational problems due to non-local weight transport during mismatch learning were described in the 1980s. Deep Learning became popular after very fast computers and huge online databases became available that enabled new applications despite these problems. Adaptive Resonance Theory, or ART, algorithms overcome the computational problems of back propagation and Deep Learning. ART is a self-organizing production system that incrementally learns, using arbitrary combinations of unsupervised and supervised learning and only locally computable quantities, to rapidly classify large non-stationary databases without experiencing catastrophic forgetting. ART classifications and predictions are explainable using the attended critical feature patterns in STM on which they build. The LTM adaptive weights of the fuzzy ARTMAP algorithm induce fuzzy IF-THEN rules that explain what feature combinations predict successful outcomes. ART has been successfully used in multiple large-scale real world applications, including remote sensing, medical database prediction, and social media data clustering. Also explainable are the MOTIVATOR model of reinforcement learning and cognitive-emotional interactions, and the VITE, DIRECT, DIVA, and SOVEREIGN models for reaching, speech production, spatial navigation, and autonomous adaptive intelligence. These biological models exemplify complementary computing, and use local laws for match learning and mismatch learning that avoid the problems of Deep Learning.
Keywords: Adaptive Resonance Theory; arm and speech movement; category learning; consciousness; deep learning; emotion; explainable AI; visual boundaries and surfaces.
Copyright © 2020 Grossberg.
Figures







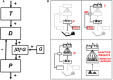
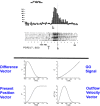

References
-
- Amari S. I. (1972). Characteristics of random nets of analog neuron-like elements. Trans. Syst. Man. Cybern. 2, 643–657. 10.1109/TSMC.1972.4309193 - DOI
-
- Bregman A. S. (1990). Auditory Scene Analysis: The Perceptual Organization of Sound. Cambridge, MA: MIT Press.
Publication types
LinkOut - more resources
Full Text Sources
Miscellaneous

