A process-based metacommunity framework linking local and regional scale community ecology

Abstract

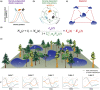
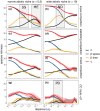
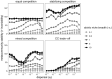
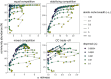
The metacommunity concept has the potential to integrate local and regional dynamics within a general community ecology framework. To this end, the concept must move beyond the discrete archetypes that have largely defined it (e.g. neutral vs. species sorting) and better incorporate local scale species interactions and coexistence mechanisms. Here, we present a fundamental reconception of the framework that explicitly links local coexistence theory to the spatial processes inherent to metacommunity theory, allowing for a continuous range of competitive community dynamics. These dynamics emerge from the three underlying processes that shape ecological communities: (1) density-independent responses to abiotic conditions, (2) density-dependent biotic interactions and (3) dispersal. Stochasticity is incorporated in the demographic realisation of each of these processes. We formalise this framework using a simulation model that explores a wide range of competitive metacommunity dynamics by varying the strength of the underlying processes. Using this model and framework, we show how existing theories, including the traditional metacommunity archetypes, are linked by this common set of processes. We then use the model to generate new hypotheses about how the three processes combine to interactively shape diversity, functioning and stability within metacommunities.

Keywords: Abiotic niche; coexistence; competition; dispersal; diversity; environmental change; functioning; stability; temporal.

Figure 1

A schematic representation of our metacommunity framework and how we formalise each aspect of it in our mathematical model. (a) Density‐independent abiotic niches of three zooplankton species are represented graphically, where r_i follows a Gaussian response curve over the gradient of abiotic environmental conditions in the metacommunity, but each species i has a different environmental optimum. (b) Dynamics also depend on interactions within and among species. This is included as per capita intraspecific α_ii interspecific α_ij interaction coefficients, and their realised impact on population dynamics increases with population size N_ix(t). Note, α_ij could be made to vary with environmental conditions, but in this paper we have assumed that it does not. (c) Dispersal alters population sizes via immigration and emigration and depends on the physical arrangement of habitat patches in the landscape. (d) Each of these processes is expressed as separate expressions in our mathematical model. In this model, N_ix(t) is the abundance of species i in patch x at time t, r_ix(t) is its density‐independent growth rate, α_ij is the per capita effect of species j on species i, I_ix(t) is the number of individuals that arrive from elsewhere in the metacommunity via immigration and E_ix(t) is the number of individuals that leave via emigration. (e) Simulated dynamics of a three zooplankton species, five lake metacommunity. The abiotic conditions vary across time and space and species respond to this heterogeneity via the Gaussian response curves in panel a. The species also compete so that the realised dynamics differ from those that would occur in the absence of interspecific competition (thick solid vs. thin dashed lines). Dispersal connects populations via immigration and emigration, with more individuals being exchanged between lakes that are in close proximity. Although stochasticity in population growth and dispersal is integral to our framework and is included in all other simulations presented in this paper, we have omitted stochasticity from these dynamics to increase clarity. Figure design by Sylvia Heredia.

Figure 2

Illustration of the three dimensions of possible metacommunity dynamics. Three key dimensions of our framework define this space: (1) density‐independent abiotic responses that range from a flat abiotic niche to narrow abiotic niches with interspecific variation in optima, (2) density‐dependent biotic interactions that vary depending on the relative strength of interspecific and intraspecific interactions and (3) dispersal that ranges from very low dispersal rates to very high dispersal rates. The approximate location of each of the four original metacommunity archetypes: ND – neutral dynamics, PD – patch dynamics, SS – species sorting and ME – mass effects, is indicated to illustrate how our framework links to previous theory. The lines below each label indicate their position in x,z space. PD_i indicates the position for competitively dominant species with lower dispersal, PD_j indicates the position for competitively weaker species with higher dispersal. Importantly, much of this space is undefined by the four archetypes, but represents potential dynamics that can emerge from different combinations of the three processes of our framework.

Figure 3

The relationship between dispersal a_i and α, β (spatial and temporal) and γ‐richness under narrow (column ‐ σ_i = 0.5) and flat (column ‐ σ_i = 10) abiotic niches across the four competitive scenarios (rows). The corresponding parameter space for each of the original metacommunity archetypes: ND – neutral dynamics, PD – patch dynamics, SS – species sorting and ME – mass effects, is indicated with the shaded boxes. The interquartile range (bands) and median (solid lines) from 30 replicate simulations are shown.

Figure 4

α, β (spatial and temporal) and γ‐richness (columns) across the full range of dispersal rates a_i (x‐axis), abiotic niche breadth σ_i (y‐axis) and competitive scenarios (rows). Each pixel represents the median value across 30 replicate simulation runs. Colour hues are spaced on a log₁₀ scale (see legend). White space represents combinations of parameters where fewer than 10 replicates resulted in species persistence. To see the dynamics that produce these patterns check out our interactive shiny app ‐ https://shiney.zoology.ubc.ca/pthompson/meta_com_shiny/.

Figure 5

The spatial insurance relationship between dispersal and metacommunity scale stability in total biomass (invariability). Lines connect different dispersal rates a_i with the same abiotic niche breadth σ_i (colour of lines and points). Values are medians from 30 replicate simulations. Legend shows the grey scale using a subset of σ_i values.

Figure 6

The biodiversity functioning relationship between α‐richness and community abundance N. Lines connect different dispersal rates a_i (colour of point) with the same abiotic niche breadth σ_i (shade of line). Values are medians from 30 replicate simulations. Legend shows the grey scale using a subset of σ_i values and the colour scale using a subset of a_i values.