Observation of the geometric phase effect in the H+HD→H2+D reaction below the conical intersection

Abstract

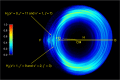
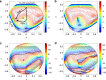
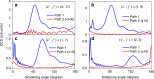
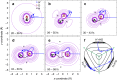
It has long been known that there is a conical intersection (CI) between the ground and first excited electronic state in the H₃ system. Its associated geometric phase (GP) effect has been theoretically predicted to exist below the CI since a long time. However, the experimental evidence has not been established yet and its dynamical origin is waiting to be elucidated. Here we report a combined crossed molecular beam and quantum reactive scattering dynamics study of the H+HD → H₂+D reaction at 2.28 eV, which is well below the CI. The GP effect is clearly identified by the observation of distinct oscillations in the differential cross section around the forward direction. Quantum dynamics theory reveals that the GP effect arises from the phase alteration of a small part of the wave function, which corresponds to an unusual roaming-like abstraction pathway, as revealed by quasi-classical trajectory calculations.

Fig. 1. Experimental image.

The experimental image of the D product from the H+HD → H₂+D reaction at 2.28 eV. “H”, “HD” and “CM” denote the velocity vectors of H beam, HD molecular beam and the origin of center of mass frame, respectively, relative to the origin of the laboratory coordinate system. The crossing angle of the H and HD beams is set to 160°. The forward (0°) and the backward (180°) scattering directions for the H₂ coproduct are defined in the center-of-mass frame relative to the H-atom beam direction, and are denoted as “F” and “B” in the image, respectively. The ro-vibrational states of H₂ products are pointed out by arrows and labeled as H₂ (v′ = 0, j′ = 11 & v′ = 1, j′ = 7) and H₂ (v′ = 1, j′ = 9 & v' = 2, j′ = 3). The normalized intensity of the image is defined by the color scale on the left of the image.

Fig. 2. Product angular distributions.

The experimental (EXP) and theoretical (NGP and GP) DCSs in the forward scattering direction for the H₂ products in the H+HD (v = 0, j = 0) → H₂+D reaction at 2.28 eV. a and c Product ro-vibrational states are (v′, j′) = (0, 11) & (1, 7); b and d Product ro-vibrational states are (v′, j′) = (1, 9) & (2, 3). “&” connects two ro-vibrational states with very small energy differences, that correspond to the rings labeled by yellow arrows in the image (see Fig. 1 and Supplementary Fig. 3). The experimental errors standard deviation (SD) are displayed in gray. The theoretical results (blue lines) in panels a and b do not include the geometric phase (NGP), while the theoretical results (blue lines) in panels c and d do include it (GP).

Fig. 3. Wavefunction analysis of the GP effect.

a The scattering wave function|ψ(ρ, θ, χ; E_c)|² in logarithmic scale (base 10) of the NGP calculations in the H + HD → H₂ + D reaction at 2.28 eV of adiabatic ground state at hyperradius ρ ≈ 2.5 bohr, where x = sin(θ)cos(2χ) and y = sin(θ)sin(2χ), along with the adiabatic ground potential energy surface. b Similar to that in Panel (a) but for the wave function of the GP calculation. The color scales on the right denote the intensities of the wave function (in logarithmic scale) in (a) and (b); c The phase of the wave function in (a) in degrees; d The phase of wave function in (b) in degrees. The color scales on the right denote the phase values in (c) and (d). “X” in the wave function patterns denotes the position of the conical intersection. “Path 1” and “Path 2” represent the reaction paths which experience one and two transition states, respectively.

Fig. 4. Relative differential cross sections from Path 1 and Path 2.

a for product H₂ (v′ = 0, j′ = 11), b (v′ = 1, j′ = 9), c (v′ = 1, j′ = 7), and d (v′ = 2, j′ = 3). “Path 1” and “Path 2” represent the reaction paths showed in Fig. 3a, which experience one and two transition states, respectively.

Fig. 5. Representative trajectories.

The representative trajectories for the forward scattering of the H + HD → H₂ (v′ = 2, j′ = 3) + D reaction are presented. The incoming H atom is labeled as H′ in the figure to distinguish from the H atom in the reactant HD molecule. a–e The roaming-like abstraction reaction (Path 2) trajectory moving with time in Cartesian coordinates with forward scattering (θ = 5°). The blue, brown, and black curves represent the trajectories of incoming H atom, the D and H atom of the reactant HD molecule, respectively, and the blue, brown, and black arrows draw the motion direction of the corresponding atoms. The positions of the H′, D, and H atoms are plotted as blue, brown, and black circles on the contour, respectively, at a series of frames with fixed time intervals located at the center of the mass of the reactant HD molecule. The contour of the potential energy surface is at instant time 23.0, 30.5, 39.0, 46.5, and 54.0 fs for frames a–e, respectively. Crosses (×) in dark gray color denotes the location of the conical intersection. f The trajectory (blue line) in a–e in hyperspherical coordinates, which experiences two transition states. The dark gray cross indicates the system’s conical intersection, “T” in green represent the three transition states. and the corresponding green lines separate three different atom-diatom channels.