Controlling a complex system near its critical point via temporal correlations
- PMID: 32699316
- PMCID: PMC7376152
- DOI: 10.1038/s41598-020-69154-0
Controlling a complex system near its critical point via temporal correlations
Abstract
Many complex systems exhibit large fluctuations both across space and over time. These fluctuations have often been linked to the presence of some kind of critical phenomena, where it is well known that the emerging correlation functions in space and time are closely related to each other. Here we test whether the time correlation properties allow systems exhibiting a phase transition to self-tune to their critical point. We describe results in three models: the 2D Ising ferromagnetic model, the 3D Vicsek flocking model and a small-world neuronal network model. We demonstrate that feedback from the autocorrelation function of the order parameter fluctuations shifts the system towards its critical point. Our results rely on universal properties of critical systems and are expected to be relevant to a variety of other settings.
Conflict of interest statement
The authors declare no competing interests.
Figures
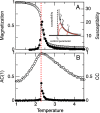
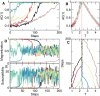

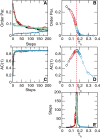
References
-
- Bak P. How Nature Works: The Science of Self-organized Criticality. New York: Springer; 1996.
-
- Chialvo DR. Emergent complex neural dynamics. Nat. Phys. 2010;6:744. doi: 10.1038/nphys1803. - DOI
-
- Mora T, Bialek W. Are biological systems poised at criticality? J. Stat. Phys. 2011;144:268. doi: 10.1007/s10955-011-0229-4. - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

