SEIR model for COVID-19 dynamics incorporating the environment and social distancing

Abstract

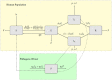
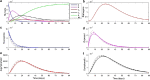
Objective: Coronavirus disease 2019 (COVID-19) is a pandemic respiratory illness spreading from person-to-person caused by a novel coronavirus and poses a serious public health risk. The goal of this study was to apply a modified susceptible-exposed-infectious-recovered (SEIR) compartmental mathematical model for prediction of COVID-19 epidemic dynamics incorporating pathogen in the environment and interventions. The next generation matrix approach was used to determine the basic reproduction number [Formula: see text]. The model equations are solved numerically using fourth and fifth order Runge-Kutta methods.

Results: We found an [Formula: see text] of 2.03, implying that the pandemic will persist in the human population in the absence of strong control measures. Results after simulating various scenarios indicate that disregarding social distancing and hygiene measures can have devastating effects on the human population. The model shows that quarantine of contacts and isolation of cases can help halt the spread on novel coronavirus.

Keywords: Basic reproduction number; COVID-19 dynamics; Mathematical model; Runge–Kutta method; SEIR model; Social distancing.

Fig. 1

SEIR-P model of COVID-19 transmission. Depicting a human (SEIR, yellow shade) and pathogen (P, green shade) compartmental model

Fig. 2

The simulated humans and pathogens populations are shown in (a, b) respectively. Effects of the constants ${\alpha }_1$ and ${\alpha }_2$ which determines the rate of new infections, are shown in (c–f): ${\alpha }_1=0.1,{\alpha }_2=0.1$, is depicted by the continuous line, ${\alpha }_1=0.05,{\alpha }_2=0.1$ is depicted by the dashed line, and ${\alpha }_1=0.1,{\alpha }_2=0.05$ is depicted by the dotted line