Comparison of parameter optimization methods for quantitative susceptibility mapping
- PMID: 32738103
- PMCID: PMC7722179
- DOI: 10.1002/mrm.28435
Comparison of parameter optimization methods for quantitative susceptibility mapping
Abstract
Purpose: Quantitative Susceptibility Mapping (QSM) is usually performed by minimizing a functional with data fidelity and regularization terms. A weighting parameter controls the balance between these terms. There is a need for techniques to find the proper balance that avoids artifact propagation and loss of details. Finding the point of maximum curvature in the L-curve is a popular choice, although it is slow, often unreliable when using variational penalties, and has a tendency to yield overregularized results.
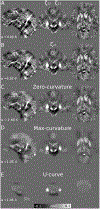
Methods: We propose 2 alternative approaches to control the balance between the data fidelity and regularization terms: 1) searching for an inflection point in the log-log domain of the L-curve, and 2) comparing frequency components of QSM reconstructions. We compare these methods against the conventional L-curve and U-curve approaches.
Results: Our methods achieve predicted parameters that are better correlated with RMS error, high-frequency error norm, and structural similarity metric-based parameter optimizations than those obtained with traditional methods. The inflection point yields less overregularization and lower errors than traditional alternatives. The frequency analysis yields more visually appealing results, although with larger RMS error.
Conclusion: Our methods provide a robust parameter optimization framework for variational penalties in QSM reconstruction. The L-curve-based zero-curvature search produced almost optimal results for typical QSM acquisition settings. The frequency analysis method may use a 1.5 to 2.0 correction factor to apply it as a stand-alone method for a wider range of signal-to-noise-ratio settings. This approach may also benefit from fast search algorithms such as the binary search to speed up the process.
Keywords: QSM; alternating direction method of multipliers (ADMM); augmented Lagrangian; total variation.
© 2020 International Society for Magnetic Resonance in Medicine.
Figures



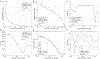
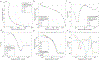


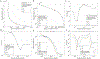

References
-
- Haacke EM, Brown R, Thompson M, Venkatesan R. Magnetic Resonance Imaging: Physical Principles and Sequence Design.
-
- Salomir R, De Senneville BD, Moonen CTW. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts Magn Reson. 2003;19B(1):26–34. doi:10.1002/cmr.b.10083 - DOI
-
- Marques JPP, Bowtell R. Application of a fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concepts Magn Reson Part B Magn Reson Eng. 2005;25(1):65–78. doi:10.1002/cmr.b.20034 - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

