Robust entanglement of an asymmetric quantum dot molecular system in a Josephson junction

Abstract

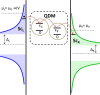
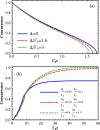
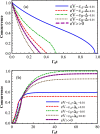
We demonstrate the generation of robust entanglement of a quantum dot molecular system in a voltage-controlled junction. To improve the quantum information characteristics of this system, we propose an applicable protocol which contains the implementation of asymmetric quantum dots as well as the engineering of reservoirs. Quantum dots can provide asymmetric coupling coefficients due to the tunable energy barriers through the gap voltage changes. To engineer the reservoirs, superconducting leads are used to prepare a voltage-biased Josephson junction. The high-controllability properties of this system give the arbitrary magnitude of entanglement by the arrangement of parameters. Significantly, the perfect entanglement can be achieved for an asymmetric structure in response to the increase of bias voltage, and also it continues saturated with the near-unit amount.

Keywords: Josephson junction; Quantum dot molecule; Quantum entanglement; Quantum mechanics; Quantum transport; Superconductors.

Figure 1

The proposed physical system: A quantum dot molecule system consists of two coupled quantum dots, A and B, with inter-dot coupling strength t_AB and QD-lead coupling strengths: T_AL, T_AR, T_BR, T_BL. The superconducting leads with the superconducting energy gaps Δ_L and Δ_R are under the bias voltage V.

Figure 2

The density of states in the superconducting reservoirs of Sc_L/QDM/Sc_R junction. The asymmetric applied bias voltage, eV = μ_L − μ_R, lets carriers to flow from the left reservoir to the QDM and then to the right lead.

Figure 3

Current-voltage characteristics in specific superconducting energy gaps. Normal leads: Solid line Δ = 0, Superconducting leads: Dashed line $\frac{\mathrm{\Delta }}{{\mathrm{\Gamma }}_0}=1.8$, Dot-dashed $\frac{\mathrm{\Delta }}{{\mathrm{\Gamma }}_0}=2.6$ for Γ₀ = πN_F|T|², $I_0=e\frac{{\mathrm{\Gamma }}_0}{ħ}$ and Δ_L = Δ_R = Δ.

Figure 4

Configuration of the initial states of two spinless electrons of molecular double quantum dot. (a): QD_A is occupied in the ground state |g_A〉 and QD_B is occupied in the ground state |g_B〉, (b): QD_A is occupied in the excited state |e_A〉 and QD_B is occupied in the excited state |e_B〉, (c): QD_A is occupied in the ground state |g_A〉 and QD_B is occupied in the excited state |e_B〉, (d): QD_A is occupied in the excited state |e_A〉 and QD_B is occupied in the ground state |g_B〉.

Figure 5

Concurrence-voltage characteristics for Panel (a): symmetric structure with κ = 0 and Panel (b): asymmetric structure with κ = 0.95; Γ₀ = πN_F|T|².

Figure 6

Time evolution of concurrence for the constant low bias voltage, Panel (a): the symmetric structure with κ = 0 and Panel (b): the asymmetric structure with κ = 0.95; Γ₀ = πN_F|T|².

Figure 7

Dynamics of concurrence for bias voltages in resonant with QD's energy levels, panel (a) for the symmetric structure with Δ_L = Δ_R = Δ and panel (b) for the asymmetric structure. Solid line: left side of the first resonant point, Dashed line: right side of the first resonant point, Dot-dashed line: left side of the second resonant point, Dotted line: right side of the second resonant point and Thick-dashed line: high bias; Γ₀ = πN_F|T|².