Geometric anomaly detection in data
- PMID: 32747569
- PMCID: PMC7443892
- DOI: 10.1073/pnas.2001741117
Geometric anomaly detection in data
Abstract
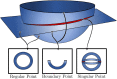
The quest for low-dimensional models which approximate high-dimensional data is pervasive across the physical, natural, and social sciences. The dominant paradigm underlying most standard modeling techniques assumes that the data are concentrated near a single unknown manifold of relatively small intrinsic dimension. Here, we present a systematic framework for detecting interfaces and related anomalies in data which may fail to satisfy the manifold hypothesis. By computing the local topology of small regions around each data point, we are able to partition a given dataset into disjoint classes, each of which can be individually approximated by a single manifold. Since these manifolds may have different intrinsic dimensions, local topology discovers singular regions in data even when none of the points have been sampled precisely from the singularities. We showcase this method by identifying the intersection of two surfaces in the 24-dimensional space of cyclo-octane conformations and by locating all of the self-intersections of a Henneberg minimal surface immersed in 3-dimensional space. Due to the local nature of the topological computations, the algorithmic burden of performing such data stratification is readily distributable across several processors.
Keywords: persistent cohomology; singularities; stratification inference.
Copyright © 2020 the Author(s). Published by PNAS.
Conflict of interest statement
The authors declare no competing interest.
Figures



References
-
- Fefferman C., Mitter S., Narayanan H., Testing the manifold hypothesis. J. Am. Math. Soc. 29, 983–1049 (2016).
-
- Lee J. A., Verleysen M., Nonlinear Dimensionality Reduction (Springer-Verlag, 2008).
-
- Ringner Markus., What is principal component analysis?. Nat. Biotechnol. 26, 303–304 (2008). - PubMed
-
- Tenenbaum J. B., De Silva V., Langford J. C., A global geometric framework for nonlinear dimensionality reduction. Science 290, 2319–2323 (2000). - PubMed
-
- Sebastian Seung H., Lee D. D., The manifold ways of perception. Science 290, 2268–2269 (2000). - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources

