Geometric mixing
- PMID: 32762434
- PMCID: PMC7422868
- DOI: 10.1098/rsta.2020.0168
Geometric mixing
Abstract
Mixing fluids often involves a periodic action, like stirring one's tea. But reciprocating motions in fluids at low Reynolds number, in Stokes flows where inertia is negligible, lead to periodic cycles of mixing and unmixing, because the physics, molecular diffusion excepted, is time reversible. So how can fluid be mixed in such circumstances? The answer involves a geometric phase. Geometric phases are found everywhere in physics as anholonomies, where after a closed circuit in the parameters, some system variables do not return to their original values. We discuss the geometric phase in fluid mixing: geometric mixing. This article is part of the theme issue 'Stokes at 200 (part 2)'.
Keywords: belly phase; fluid mixing; geometric phase; journal-bearing flow.
Conflict of interest statement
We declare we have no competing interests.
Figures
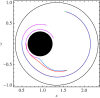


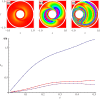
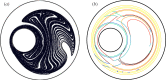



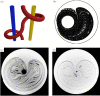


References
-
- Stokes GG. 1851. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Phil. Soc. 9, 8–106.
-
- Taylor GI. 1960. Low Reynolds number flow. Scotsdale, AZ: Educational Services Incorporated. (16 mm film).
-
- Heller JP. 1960. An unmixing demonstration. Am. J. Phys. 28, 348–353. (10.1119/1.1935802) - DOI
-
- Shapere A, Wilczek F eds. 1989. Geometric phases in physics. Singapore: World Scientific.
-
- Berry MV. 1984. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57. (10.1098/rspa.1984.0023) - DOI
LinkOut - more resources
Full Text Sources

