Chemotaxis strategies of bacteria with multiple run modes

Abstract

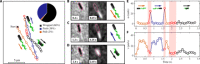
Bacterial chemotaxis-a fundamental example of directional navigation in the living world-is key to many biological processes, including the spreading of bacterial infections. Many bacterial species were recently reported to exhibit several distinct swimming modes-the flagella may, for example, push the cell body or wrap around it. How do the different run modes shape the chemotaxis strategy of a multimode swimmer? Here, we investigate chemotactic motion of the soil bacterium Pseudomonas putida as a model organism. By simultaneously tracking the position of the cell body and the configuration of its flagella, we demonstrate that individual run modes show different chemotactic responses in nutrition gradients and, thus, constitute distinct behavioral states. On the basis of an active particle model, we demonstrate that switching between multiple run states that differ in their speed and responsiveness provides the basis for robust and efficient chemotaxis in complex natural habitats.

Fig. 1. A combined F-L/P-C microscopy technique enables tracking of the multimode swimmer P. putida with simultaneous information on cell position and orientation of the flagellar bundle.

(A) A typical trajectory containing multiple changes of the flagellar configuration. Cell body positions are displayed by circular markers at 0.1-s intervals. The three run modes are highlighted in color: pull (orange), push (blue), and wrapped (black). A schematic of the flagellar bundle configuration is placed close to the corresponding part of the trajectory (not drawn to scale). The arrows indicate the swimming direction. The transition events, identified by the tumble analysis, are shown in red. The frequency of observations of the different swimming modes is represented as an inset (built from 2642 runs in total). The panels in the middle (B to D) represent the corresponding image series of P-C (left) and F-L (middle) with the time delay of 0.05 s between two consecutive P-C and F-L images. The swim modes are symbolized by cartoons on the right. The pink ellipses are the position of the cell body, obtained by linear interpolation between adjacent P-C images. (E and F) Time series of the absolute value of the rotational velocity ω (E) and the swimming speed v (F) [same color scheme as in (A)]. Scale bars, 5 μm.

Fig. 2. Statistics of the turn angles of P. putida in the bulk for transitions from one run mode to another.

(A) Narrow turn angle distribution centered around zero degree corresponding to motor stops during push runs; (B) broad distribution of turn angles with a characteristic peak around 60° for transitions from wrapped to wrapped mode; (C) and (D) reveal that reversals of the direction of motion (peak at 180°) occur whenever the swimming mode changes from push to wrapped and vice versa. Dashed lines represent the median values. Distributions are built from 59, 415, 266, and 199 events for the histograms (A to D), respectively.

Fig. 3. Run-time bias of P. putida in a linear concentration gradient.

The plots show the sojourn probabilities s(t) that a run is longer than a given time t for runs in the push mode (A) and wrapped mode (B). Upgradient runs are shown in blue and downgradient runs in red. The control experiments in the absence of a gradient are plotted in gray for comparison. The error bars indicate the 1σ interval estimated by bootstrapping (34). The run-time bias depends on the swim mode: Whereas the run-time statistics up- and downgradient is practically indistinguishable for bacteria swimming in the push mode, there is a significant run-time bias in the wrapped mode; bacteria in the wrapped mode tend to decrease the downgradient run time. Each curve includes information from at least 900 runs.

Fig. 4. Model representation of the motility pattern of P. putida: The two essential run states, push and wrap, are interrupted by stops of the flagellar driving or their reconfiguration with respect to the cell body inducing transitions from one run mode to another accompanied by turns.

The mean duration of all states is parameterized by inverse transition rates, denoted by κ_i. The parameter p_pw reflects the probability that the push mode is followed by the wrapped mode (and vice versa for p_wp).

Fig. 5. Quantitative prediction and parameter study of the long-time chemotaxis response of P. putida.

(A) Response function μ_w as a function of the transition probability p_wp from the wrapped to the push mode (we set p_pw = 1 − p_wp). For p_wp = 0, bacteria stay in the wrapped mode and perform run-and-turn motility. In the opposite limit (p_wp = 1), they perform push runs that are occasionally interrupted by stops. The dependence of μ_w on p_wp is not monotonic, and all curves intersect around p_wp ≈ 0.35, reflecting a robust chemotactic response independent of the turn statistics ⟨cos ψ_ww⟩. Parameters: Average turn angles ⟨cos ψ_pp⟩ = 0.9, ⟨cos ψ_pw⟩ = − 0.9, and ⟨cos ψ_wp⟩ = − 0.9; speeds v_p = 25 μm/s and v_w = 13 μm/s; average reorientation rates λ_p = 0.3 s⁻¹ and λ_w = 0.4 s⁻¹; rotational diffusion D_p = 0.03 s⁻¹ and D_w = 0.13 s⁻¹; and spatial dimension d = 3. (B) Chemotaxis in heterogeneous environments. The plot shows the relative difference Λ_μ of the response functions μ_p and μ_w as a function of the mean free path length in a disordered environment. If the obstacle density is low (large mean free path length), then the faster run mode is the beneficial one. However, as collisions become more frequent, i.e., if the mean free path is comparable to the average run times, both run modes are equally efficient. In crowded environments, where l_c is smaller than the average run length, the wrapped mode may even become the more efficient one (Λ_μ < 0). Parameters: Mean turn angles for collision with obstacles ⟨cos ψ_c⟩ = − 0.3, p_pw = 0.7, and p_wp = 0.4; other parameters as in (A). On the basis of the data, we estimated 0.2 ≤ ⟨cos ψ_ww⟩ ≤ 0.6 for P. putida, represented by solid lines in both panels.