Comparative infection modeling and control of COVID-19 transmission patterns in China, South Korea, Italy and Iran

Abstract

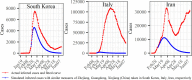
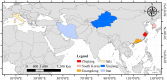
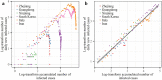
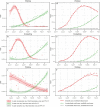
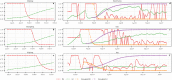
The COVID-19 has become a pandemic. The timing and nature of the COVID-19 pandemic response and control varied among the regions and from one country to the other, and their role in affecting the spread of the disease has been debated. The focus of this work is on the early phase of the disease when control measures can be most effective. We proposed a modified susceptible-exposed-infected-removed model (SEIR) model based on temporal moving windows to quantify COVID-19 transmission patterns and compare the temporal progress of disease spread in six representative regions worldwide: three Chinese regions (Zhejiang, Guangdong and Xinjiang) vs. three countries (South Korea, Italy and Iran). It was found that in the early phase of COVID-19 spread the disease follows a certain empirical law that is common in all regions considered. Simulations of the imposition of strong social distancing measures were used to evaluate the impact that these measures might have had on the duration and severity of COVID-19 outbreaks in the three countries. Measure-dependent transmission rates followed a modified normal distribution (empirical law) in the three Chinese regions. These rates responded quickly to the launch of the 1^st-level Response to Major Public Health Emergency in each region, peaking after 1-2 days, reaching their inflection points after 10-19 days, and dropping to zero after 11-18 days since the 1^st-level response was launched. By March 29^th, the mortality rates were 0.08% (Zhejiang), 0.54% (Guangdong) and 3.95% (Xinjiang). Subsequent modeling simulations were based on the working assumption that similar infection transmission control measures were taken in South Korea as in Zhejiang on February 25^th, in Italy as in Guangdong on February 25^th, and in Iran as in Xinjiang on March 8^th. The results showed that by June 15^th the accumulated infection cases could have been reduced by 32.49% (South Korea), 98.16% (Italy) and 85.73% (Iran). The surface air temperature showed stronger association with transmission rate of COVID-19 than surface relative humidity. On the basis of these findings, disease control measures were shown to be particularly effective in flattening and shrinking the COVID-10 case curve, which could effectively reduce the severity of the disease and mitigate medical burden. The proposed empirical law and the SEIR-temporal moving window model can also be used to study infectious disease outbreaks worldwide.

Keywords: COVID-19; Climatic factors; Distancing measures; Dynamic; SEIR; Transmission rate.

Graphical abstract

Fig. 1

Temporal evolution of accumulated and cured cases of COVID-19 diseases in Zhejiang, Guangdong and Xinjiang of China, South Korea, Italy and Iran. Major events concerning disease control and prevention are labeled at their corresponding date.

Fig. 2

Geographical locations of the six study regions.

Fig. 3

Outline of the workflow in this study.

Fig. 4

Relationship between the numbers of daily new infected cases vs. the accumulated numbers of infected cases. (a) Scatter-plots of this relationship for the six regions; (b) linear fitting of the scatter-plots with 95% confidence interval shown as shaded areas (excluding points showing declining trends or where the number of daily new infected cases ≤10).

Fig. 5

SEIR modeling results in the three Chinese regions. The first column displays the empirical transmission rates (red dots), cure rates (green dots) and mortality rates (gray dots) together with the corresponding fitted lines and the 95% confidence interval (shadows) in Zhejiang, Guangdong and Xinjiang (China); the second column displays the reported infected case numbers (red dots), accumulated cured case numbers (green dots) and dead case numbers (gray dots) together with the corresponding SEIR-produced values (lines) in the three Chinese regions. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 6

SEIR modeling results in South Korea, Italy and Iran. The first column displays empirical values of the three rates together with the transmission rates based on simulations of the Chinese control measures assumed since February 25^th, February 25^th and March 8^th in South Korea, Italy and Iran, respectively; and the second column displays the reported numbers, SEIR-produced values and the simulated infected case numbers in the three countries.

Fig. 7

The trends of R₀(t) and L₀(t) variations in each of the six study regions (for better visualization, we set R₀(t) = 1 whenever the R₀(t) value was computed to be greater than 1).