Longevity and the drift barrier: Bridging the gap between Medawar and Hamilton

Abstract

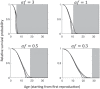
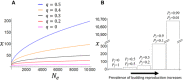
Most organisms have finite life spans. The maximum life span of mammals, for example, is at most some years, decades, or centuries. Why not thousands of years or more? Can we explain and predict maximum life spans theoretically, based on other traits of organisms and associated ecological constraints? Existing theory provides reasons for the prevalence of ageing, but making explicit quantitative predictions of life spans is difficult. Here, I show that there are important unappreciated differences between two backbones of the theory of senescence: Peter Medawar's verbal model, and William Hamilton's subsequent mathematical model. I construct a mathematical model corresponding more closely to Medawar's verbal description, incorporating mutations of large effect and finite population size. In this model, the drift barrier provides a standard by which the limits of natural selection on age-specific mutations can be measured. The resulting model reveals an approximate quantitative explanation for typical maximum life spans. Although maximum life span is expected to increase with population size, it does so extremely slowly, so that even the largest populations imaginable have limited ability to maintain long life spans. Extreme life spans that are observed in some organisms are explicable when indefinite growth or clonal reproduction is included in the model.

Keywords: Evolution of ageing; genetic drift; senescence; theory.

Figure 1

The effects of recruitment, age at first reproduction, and population size on the evolution of maximum life span. The curves are analytical results based on the discrete equation 3, which is more efficient to simulate than the continuous equation 2. Dots are results of simulations that intentionally violate assumptions of the analytical model to check for robustness (see model description in the main text and code in the SI). Mutations arise in every generation so that there are always multiple alleles in the population, and each mutation can increase or decrease life span by a randomly picked amount proportional to current life span. The gamma distribution is parameterised so that on average 1 mutation in 100 is advantageous (i.e., increases maximum life span). However, all mutations still result in certain death at the age thus determined; this assumption is relaxed in Figure 2. Each instance of the simulation was run for 1 million generations (panel A) or 4 million generations (panel B, to account for larger population sizes) in multiples of generation time, and the coloured dots indicate averages of the last 30% of these generations. Note that the curves in panel A are not exact vertically shifted copies of each other as one might first expect from equations (2), (3). The reason for this is that age at first reproduction alters $N_e$ when overlapping generations are present. $N_e$ for the analytical results was calculated following Hill (1979). In panel A, the adult population size is 1600 individuals, and in panel B age at first reproduction is 1. The open circles in panel B are simulation results where fluctuations of large magnitude in population size were allowed around the mean (see Supporting Information). Population persistence in the presence of these fluctuations requires sufficiently high per‐capita recruitment, hence these results are restricted to the two lowest curves in panel B.

Figure 2

Simulation results and the selection shadow as predicted by equation 3. In contrast to Figure 1, mutations are now typically not lethal, and instead alter age‐specific survival probability at population regulation. A mutation is picked from a gamma distribution (Eyre‐Walker & Keightley 2007) in every generation as in Figure 1, but manifests its effect in a very different way (see methods and Supporting Information). Simulations were run for 1 million generations, and the figures represent the evolved age‐specific survival weightings averaged over the last 30% of these generations. A weighting of 1 is the maximum value (i.e., highest possible survival probability), whereas a weighting of 0 implies certain death at population regulation. The gray zone illustrates the ages where the analytical equation 3 predicts drift to overwhelm selection (hence expected to be an approximate limit to longevity). The three partially overlapping curves within each panel result from mutation distributions parameterized so that on average 1 in 200, 1 in 100, and 1 in 10 mutations are beneficial, moving from leftmost to rightmost curve within each panel (see methods and Supporting Information for details and illustrations of mutation distributions). In all panels, effective population size is 1600 individuals and age at first reproduction is 1 (however, only adult life span is included in the x‐axis).

Figure 3

Evolution of extraordinary life spans. In the analytical results of panel A, extrinsic mortality decreases over the adult lifetime, for example, due to indeterminate growth. Age‐specific extrinsic mortality is modeled in this example as $\frac{\mu }{1+q(\tau -b)}$, where $\tau$ is age and q is a parameter that determines the strength of age‐specific extrinsic mortality decrease. Repeating the derivation of equation 2 with this assumption obtains $x=b+\frac{{N_e}^{\frac{q}{\sigma f}}-1}{q}$ (see Supporting Information for derivation). The stronger the decrease in extrinsic mortality with age, the higher the temporal drift barrier and evolving maximum life span x. The lowermost line (q = 0) corresponds to equation 2 with constant adult extrinsic mortality. In panel B, reproduction takes place partially via outgrowths or fragments of the parent (e.g., budding), and these fragments are assumed to inherit their parents biological age, that is, they are “born older” than offspring originating from gametic reproduction. Budding reproduction alternates with gametic reproduction where age is not inherited. The bars represent different autocorrelations for reproductive mode. p ₁ is transition probability from gametic to budding reproduction, whereas p ₂ is the transition probability from budding to gametic reproduction. Hence, budding reproduction is absent in the leftmost bar, whereas budding dominates the lifecycle in the rightmost bar. Note the break in the y‐axis. The lack of “resetting” of biological age in budding reproduction makes late‐acting mutations visible to selection, and there is no limit to how far life span can evolve as the prevalence of budding increases. Apart from transitions between the two reproductive modes, the simulation used to generate panel B is similar to Figure 1. See Supporting Information for simulation code. In both panels $N_e=1600$ and $b=\sigma =f=1$.