Mechanisms and modeling of electrohydrodynamic phenomena
- PMID: 32782978
- PMCID: PMC7415859
- DOI: 10.18063/ijb.v5i1.166
Mechanisms and modeling of electrohydrodynamic phenomena
Erratum in
-
ERRATUM.Int J Bioprint. 2020 Sep 17;6(4):309. doi: 10.18063/ijb.v6i4.309. eCollection 2020. Int J Bioprint. 2020. PMID: 33102924 Free PMC article.
Abstract
The purpose of this paper is to review the mechanisms of electrohydrodynamic (EHD) phenomenon. From this review, researchers and students can learn principles and development history of EHD. Significant progress has been identified in research and development of EHD high-resolution deposition as a direct additive manufacturing method, and more effort will be driven to this direction soon. An introduction is given about current trend of additive manufacturing and advantages of EHD inkjet printing. Both theoretical models and experiment approaches about the formation of cone, development of cone-jet transition and stability of jet are presented. The formation of a stable cone-jet is the key factor for precision EHD printing which will be discussed. Different scaling laws can be used to predict the diameter of jet and emitted current in different parametrical ranges. The information available in this review builds a bridge between EHD phenomenon and three-dimensional high-resolution inkjet printing.
Keywords: Electrohydrodynamic; additive manufacturing; cone-jet; inkjet printing; jet stability.
Copyright: © 2019 Gao D, et al.
Figures


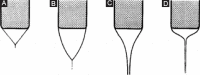
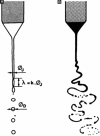
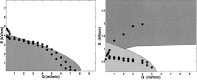
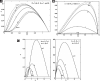

References
-
- Onses M S, Sutanto E, Ferreira PM, et al. Mechanisms, capabilities, and applications of high-resolution electrohydrodynamic jet printing. Small J. 2015;11(34):4237–4266. https://doi.org/10.1002/smll.201500593;https://doi.org/10.1002/smll.2015.... - PubMed
-
- Korkut S, Saville D A, Aksay I A. Collodial cluster arrays by electrohydrodynamic printing. Langmuir. 2008;24:12196–12201. https://doi.org/10.1021/la8023327. - PubMed
-
- Chrisey D B. Materials processing:The power of direct writing. Science. 2000;289(5481):879–881. https://doi.org/10.1126/science.289.5481.879. - PubMed
-
- Jaworek A, Sobczyk A. Electrospraying route to nanotechnology:An overview. J Electrostat. 2008;66(3–4):197–219. https://doi.org/10.1016/j.elstat.2007.10.001.
-
- Chen C H. Vienna: Springer; 2011. Electrohydrodynamic Stability; pp. 177–220. https://doi.org/10.1007/978-3-7091-0900-7_6.
Publication types
LinkOut - more resources
Full Text Sources
