Correlated clusters of closed reaction centers during induction of intact cells of photosynthetic bacteria

Abstract

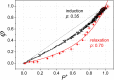
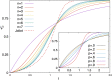
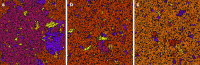
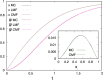
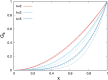
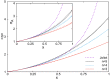
Antenna systems serve to absorb light and to transmit excitation energy to the reaction center (RC) in photosynthetic organisms. As the emitted (bacterio)chlorophyll fluorescence competes with the photochemical utilization of the excitation, the measured fluorescence yield is informed by the migration of the excitation in the antenna. In this work, the fluorescence yield concomitant with the oxidized dimer (P⁺) of the RC were measured during light excitation (induction) and relaxation (in the dark) for whole cells of photosynthetic bacterium Rhodobacter sphaeroides lacking cytochrome c₂ as natural electron donor to P⁺ (mutant cycA). The relationship between the fluorescence yield and P⁺ (fraction of closed RC) showed deviations from the standard Joliot-Lavergne-Trissl model: (1) the hyperbola is not symmetric and (2) exhibits hysteresis. These phenomena originate from the difference between the delays of fluorescence relative to P⁺ kinetics during induction and relaxation, and in structural terms from the non-random distribution of the closed RCs during induction. The experimental findings are supported by Monte Carlo simulations and by results from statistical physics based on random walk approximations of the excitation in the antenna. The applied mathematical treatment demonstrates the generalization of the standard theory and sets the stage for a more adequate description of the long-debated kinetics of fluorescence and of the delicate control and balance between efficient light harvest and photoprotection in photosynthetic organisms.

Figure 1

Kinetics of fluorescence yield ($\phi$) and absorption changes of oxidized dimer (P⁺) during induction and relaxation of whole cells of cytochrome c₂ less mutant of purple photosynthetic bacterium Rba. sphaeroides. Both $\phi$ and P⁺ are normalized to their maximum values.

Figure 2

Double reciprocal representations of the fluorescence yield ($\phi$) and oxidized dimer (P⁺) during induction and relaxation. The plots demonstrate the deviation from the Joliot model that predicts straight lines (curved in the logarithmic scale).

Figure 3

Double reciprocal plots of the fluorescence yield ($\phi$) and complementary area (C) above the fluorescence rise (induction) or below the fluorescence drop (relaxation), respectively. Systematic deviations can be observed from straight lines predicted by the Joliot model. Note, that the straight lines are curved in logarithmic scales.

Figure 4

Fluorescence yield ($\phi$) as a function of closure of the reaction centers (P⁺) during induction and relaxation phases obtained by comparison of the kinetics of fluorescence with those of the oxidised dimer by elimination of the time. The cells were harvested in the late stationary phase of their growth (3 days after inoculation). The measured points were formally approximated by curves derived from the Joliot model with different p values indicated. The straight line corresponds to $p=0$, i.e. no connection between the PSUs. The hysteresis (the difference between induction and relaxation) is relatively modest.

Figure 5

Demonstration of large hysteresis due to the increased difference between the kinetics of fluorescence yield and closure of the PSU during induction and relaxation. The bacteria were harvested in the early phase of their growth (24 h after inoculation). Otherwise the experimental conditions and evaluation of the data were the same as in Fig. 4.

Figure 6

Fluorescence yield as a function of the fraction of closed RCs calculated during relaxation (LMF calculation and MC simulations) and during induction (CMF calculation and MC simulations) at a hopping probability $p=0.9$ for $n=2$ (main panel) and $n=3$ (inset). In both cases the best fit (with p) of the Joliot theory, as well as the result with a fixed $p=0.9$ is also presented.

Figure 7

Time-dependence of the fluorescence yield calculated by the LMF approximation for various values of n at a hopping probability $p=0.9$. The result of the Joliot theory with the same p is shown for comparison. Inset: Time-dependence of the fluorescence yield in the Joliot model for different values of the hopping probability.

Figure 8

Typical cluster structures of RCs on a $200\times 200$ square lattice at an occupation probability, $x=0.594(1)$, slightly above the site-percolation threshold. Left panel: uncorrelated percolation, corresponding to the structure during relaxation with $n=1$. Middle panel: during induction with $p=0.9$ and $n=2$. Right panel: during induction with $p=0.9$ and $n=3$. Sites with the same colour represent connected clusters of closed RCs.

Figure 9

Dynamics of the order-parameter, x(t), and the fluorescence yield, $\phi (t)$, calculated for a hopping probability $p=0.9$ and for $n=2$. Results of the LMF and CMF approaches are compared with MC simulations during induction. Inset: Connected nearest-neighbour correlation function ${\tilde{x}}_2=x_2-x^2$ as a function of x for $p=0.9$ and for $n=2$. The CMF calculations perfectly overlap with the results of MC simulations.

Figure 10

k-site correlations versus fraction of closed RCs calculated in the different approaches at a hopping probability $p=0.9$. Dotted line: Joliot-theory, dashed line: LMF approach, full line: CMF approach.

Figure 11

Average number of exciton steps as a function of the fraction of closed RCs at a hopping probability $p=0.9$ calculated with the CMF approach (full line) and with the LMF approach (dashed line), for different maximal number of steps, n. With dotted line result of the Joliot-theory ($n\to \infty$) is presented. Inset: absorption cross section as a function of the fraction of closed RCs.