COVID-19 and SARS-CoV-2. Modeling the present, looking at the future
- PMID: 32834430
- PMCID: PMC7386394
- DOI: 10.1016/j.physrep.2020.07.005
COVID-19 and SARS-CoV-2. Modeling the present, looking at the future
Abstract
Since December 2019 the Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) has produced an outbreak of pulmonary disease which has soon become a global pandemic, known as COronaVIrus Disease-19 (COVID-19). The new coronavirus shares about 82% of its genome with the one which produced the 2003 outbreak (SARS CoV-1). Both coronaviruses also share the same cellular receptor, which is the angiotensin-converting enzyme 2 (ACE2) one. In spite of these similarities, the new coronavirus has expanded more widely, more faster and more lethally than the previous one. Many researchers across the disciplines have used diverse modeling tools to analyze the impact of this pandemic at global and local scales. This includes a wide range of approaches - deterministic, data-driven, stochastic, agent-based, and their combinations - to forecast the progression of the epidemic as well as the effects of non-pharmaceutical interventions to stop or mitigate its impact on the world population. The physical complexities of modern society need to be captured by these models. This includes the many ways of social contacts - (multiplex) social contact networks, (multilayers) transport systems, metapopulations, etc. - that may act as a framework for the virus propagation. But modeling not only plays a fundamental role in analyzing and forecasting epidemiological variables, but it also plays an important role in helping to find cures for the disease and in preventing contagion by means of new vaccines. The necessity for answering swiftly and effectively the questions: could existing drugs work against SARS CoV-2? and can new vaccines be developed in time? demands the use of physical modeling of proteins, protein-inhibitors interactions, virtual screening of drugs against virus targets, predicting immunogenicity of small peptides, modeling vaccinomics and vaccine design, to mention just a few. Here, we review these three main areas of modeling research against SARS CoV-2 and COVID-19: (1) epidemiology; (2) drug repurposing; and (3) vaccine design. Therefore, we compile the most relevant existing literature about modeling strategies against the virus to help modelers to navigate this fast-growing literature. We also keep an eye on future outbreaks, where the modelers can find the most relevant strategies used in an emergency situation as the current one to help in fighting future pandemics.
© 2020 Elsevier B.V. All rights reserved.
Conflict of interest statement
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures









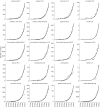


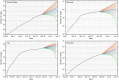





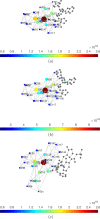


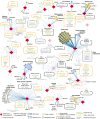









References
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

