A SIR model assumption for the spread of COVID-19 in different communities

Abstract

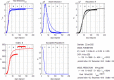
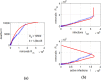
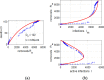
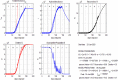
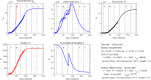
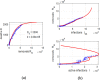
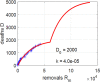
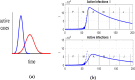
In this paper, we study the effectiveness of the modelling approach on the pandemic due to the spreading of the novel COVID-19 disease and develop a susceptible-infected-removed (SIR) model that provides a theoretical framework to investigate its spread within a community. Here, the model is based upon the well-known susceptible-infected-removed (SIR) model with the difference that a total population is not defined or kept constant per se and the number of susceptible individuals does not decline monotonically. To the contrary, as we show herein, it can be increased in surge periods! In particular, we investigate the time evolution of different populations and monitor diverse significant parameters for the spread of the disease in various communities, represented by China, South Korea, India, Australia, USA, Italy and the state of Texas in the USA. The SIR model can provide us with insights and predictions of the spread of the virus in communities that the recorded data alone cannot. Our work shows the importance of modelling the spread of COVID-19 by the SIR model that we propose here, as it can help to assess the impact of the disease by offering valuable predictions. Our analysis takes into account data from January to June, 2020, the period that contains the data before and during the implementation of strict and control measures. We propose predictions on various parameters related to the spread of COVID-19 and on the number of susceptible, infected and removed populations until September 2020. By comparing the recorded data with the data from our modelling approaches, we deduce that the spread of COVID-19 can be under control in all communities considered, if proper restrictions and strong policies are implemented to control the infection rates early from the spread of the disease.

Keywords: COVID-19; SIR model; forecasting; infectious disease; pandemic; virus spreading.

Fig. 1

China: Model predictions for the period from 22 January to 9 August, 2020 with data from January to June, 2020. The data show a discrete jump in deaths D in mid-April.

Fig. 2

China: (a) Nonlinear fitting with Eq. (3) using a trial-and-error method to estimate the number of deaths, D from the removed population, R_m (see text for the details). (b) Plots of the number of removals, R_m against the cumulative total infections I_tot and current active cases I.

Fig. 3

South Korea: Model predictions for the period from 26 February to 13 September, 2020 with data from February to June, 2020.

Fig. 4

South Korea: (a) Nonlinear fitting with Eq. (3) using a trial-and-error method to estimate the number of deaths, D from the removed population, R_m (see text for the details). (b) Plots of the number of removals, R_m against the cumulative total infections I_tot and current active cases I.

Fig. 5

India: Model predictions for the period from 14 March to 30 September, 2020 with data from March to June, 2020.

Fig. 6

India: (a) Nonlinear fitting with Eq. (3) using a trial-and-error method to estimate the number of deaths, D from the removed population, R_m (see text for the details). (b) Plots of the number of removals, R_m against the cumulative total infections I_tot and current active cases I.

Fig. 7

Australia: Model predictions for the period from 22 January to 9 August, 2020 with data from January to June, 2020.

Fig. 8

Australia: (a) Nonlinear fitting with Eq. (3) using a trial-and-error method to estimate the number of deaths, D from the removed population, R_m (see text for the details). (b) Plots of the number of removals, R_m against the cumulative total infections I_tot and current active cases I.

Fig. 9

USA: Model predictions for the period from 22 January to 9 August, 2020 with data from January to June, 2020.

Fig. 10

USA: (a) Nonlinear fitting with Eq. (3) using a trial-and-error method to estimate the number of deaths, D from the removed population, R_m (see text for the details). (b) Plots of the number of removals, R_m against the cumulative total infections I_tot and current active cases I.

Fig. 11

Texas: Model predictions for the period from 12 March to 28 September, 2020 with data from March to June, 2020.

Fig. 12

Texas: (a) Nonlinear fitting with Eq. (3) using a trial-and-error method to estimate the number of deaths, D from the removed population, R_m (see text for the details). (b) Plots of the number of removals, R_m against the cumulative total infections I_tot and current active cases I.

Fig. 13

Texas: Model predictions with a surge period occurring at the end of June, 2020.

Fig. 14

Texas: If a second wave occurs, there could be increase in the number of deaths, D.

Fig. 15

Italy: Model predictions for the period from 26 February to 13 September, 2020 with data from February to June, 2020.

Fig. 16

Italy: (a) Nonlinear fitting with Eq. (3) using a trial-and-error method to estimate the number of deaths, D from the removed population, R_m (see text for the details). (b) Plots of the number of removals, R_m against the cumulative total infections I_tot and current active cases I.

Fig. 17

Flattening the curve: Panel (a): The flattening of the curve diagram used widely in the media to represent a means of reducing the impacts of COVID-19. Panel (b) If the number of susceptible individuals is reduced, then the peak number of infections will be less and the time for the number of infections to fall to low numbers is reduced.