Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Dec:64:252-258.
doi: 10.1016/j.inffus.2020.08.002. Epub 2020 Aug 6.

The introduction of population migration to SEIAR for COVID-19 epidemic modeling with an efficient intervention strategy

Min Chen  1 , Miao Li  1 , Yixue Hao  1 , Zhongchun Liu  2 , Long Hu  1 , Lin Wang  3   4
Affiliations

The introduction of population migration to SEIAR for COVID-19 epidemic modeling with an efficient intervention strategy

Min Chen et al. Inf Fusion. 2020 Dec.

Abstract

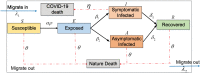
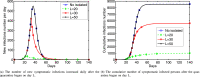
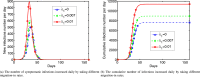
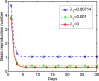
In this paper, we present a mathematical model of an infectious disease according to the characteristics of the COVID-19 pandemic. The proposed enhanced model, which will be referred to as the SEIR (Susceptible-Exposed-Infectious-Recovered) model with population migration, is inspired by the role that asymptomatic infected individuals, as well as population movements can play a crucial role in spreading the virus. In the model, the infected and the basic reproduction numbers are compared under the influence of intervention policies. The experimental simulation results show the impact of social distancing and migration-in rates on reducing the total number of infections and the basic reproductions. And then, the importance of controlling the number of migration-in people and the policy of restricting residents' movements in preventing the spread of COVID-19 pandemic are verified.

Keywords: Basic reproduction number; COVID-19; Contact rate; Migration-in rate; SEIAR.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

Fig. 1
Fig. 1
The transformation of Susceptible, Exposed, Infectious, Asymptomatic, and Recovered individuals of COVID-19 in SEIAR model with population migration.
Fig. 2
Fig. 2
The real data for SEIAR Model.
Fig. 3
Fig. 3
The impact of the initiation time of quarantine measures on the spread of COVID-19.
Fig. 4
Fig. 4
The impact of the end time of quarantine measures on the spread of COVID-19.
Fig. 5
Fig. 5
The impact of restrict migration-in on the spread of COVID-19.
Fig. 6
Fig. 6
The influence of mobility and contact rate on basic reproduction number.
See this image and copyright information in PMC

References

    1. Lekone P.E., Finkenstadt B. Statistical inference in a stochastic epidemic SEIR model with control intervention: Ebola as a case study. Biometrics. 2006;62(4):1170–1177. - PubMed
    1. Giamberardino P., Compagnucci L., De Giorgi C., Iacoviello D. Modeling the effects of prevention and early diagnosis on HIV/AIDS infection diffusion. IEEE Trans. Syst. Man Cybern.: Syst. 2019;49(10):2119–2130. doi: 10.1109/TSMC.2017.2749138. - DOI
    1. Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Charact. 2020;115(772):700–721. doi: 10.1137/S0036144500371907. - DOI
    1. Hethcote H.W. The mathematics of infectious diseases. SIAM Rev. 2000;42(4):599–653.
    1. Zuev A., Karaman D. SEIR model for transmission of dengue fever in Selangor Malaysia. 2018 International Scientific-Practical Conference Problems of InfocommunicationsSci. Technol. 2012;9(1):380–389.

LinkOut - more resources