Dynamics of a fractional order mathematical model for COVID-19 epidemic

Abstract

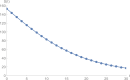
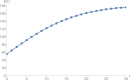
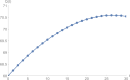
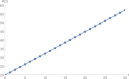
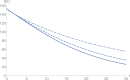
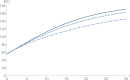
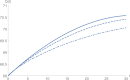
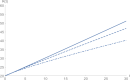
In this work, we formulate and analyze a new mathematical model for COVID-19 epidemic with isolated class in fractional order. This model is described by a system of fractional-order differential equations model and includes five classes, namely, S (susceptible class), E (exposed class), I (infected class), Q (isolated class), and R (recovered class). Dynamics and numerical approximations for the proposed fractional-order model are studied. Firstly, positivity and boundedness of the model are established. Secondly, the basic reproduction number of the model is calculated by using the next generation matrix approach. Then, asymptotic stability of the model is investigated. Lastly, we apply the adaptive predictor-corrector algorithm and fourth-order Runge-Kutta (RK4) method to simulate the proposed model. Consequently, a set of numerical simulations are performed to support the validity of the theoretical results. The numerical simulations indicate that there is a good agreement between theoretical results and numerical ones.

Keywords: Adaptive predictor–corrector algorithm; COVID-19 epidemic; Fractional differential equations; Numerical simulations; Stability analysis.

Figure 1

$S(t)$ against t: solid line presents the proposed approximation, dotted line stands for RK4 method

Figure 2

$E(t)$ versus t: solid line presents the proposed approximation, dotted line stands for RK4 method

Figure 3

$I(t)$ against t: solid line presents the proposed approximation, dotted line stands for RK4 method

Figure 4

$Q(t)$ against t: solid line presents the proposed approximation, dotted line stands for RK4 method

Figure 5

$R(t)$ against t: solid line presents the proposed approximation, dotted line stands for RK4 method

Figure 6

$S(t)$ against t: (solid line) $a=1.0$, (dot-dashed line) $a=0.85$, (dashed line) $a=0.75$

Figure 7

$E(t)$ against t: (solid line) $a=1.0$, (dot-dashed line) $a=0.85$, (dashed line) $a=0.75$

Figure 8

$I(t)$ against t: (solid line) $a=1.0$, (dot-dashed line) $a=0.85$, (dashed line) $a=0.75$

Figure 9

$Q(t)$ against t: (solid line) $a=1.0$, (dot-dashed line) $a=0.85$, (dashed line) $a=0.75$

Figure 10

$R(t)$ against t: (solid line) $a=1.0$, (dot-dashed line) $a=0.85$, (dashed line) $a=0.75$