The reproduction number of COVID-19 and its correlation with public health interventions

Abstract

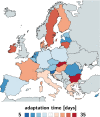
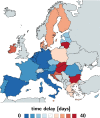
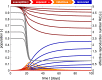
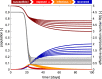
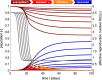
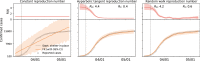
Throughout the past six months, no number has dominated the public media more persistently than the reproduction number of COVID-19. This powerful but simple concept is widely used by the public media, scientists, and political decision makers to explain and justify political strategies to control the COVID-19 pandemic. Here we explore the effectiveness of political interventions using the reproduction number of COVID-19 across Europe. We propose a dynamic SEIR epidemiology model with a time-varying reproduction number, which we identify using machine learning. During the early outbreak, the basic reproduction number was 4.22 ± 1.69, with maximum values of 6.33 and 5.88 in Germany and the Netherlands. By May 10, 2020, it dropped to 0.67 ± 0.18, with minimum values of 0.37 and 0.28 in Hungary and Slovakia. We found a strong correlation between passenger air travel, driving, walking, and transit mobility and the effective reproduction number with a time delay of 17.24 ± 2.00 days. Our new dynamic SEIR model provides the flexibility to simulate various outbreak control and exit strategies to inform political decision making and identify safe solutions in the benefit of global health.

Keywords: COVID-19; Epidemiology; Machine learning; Reproduction number; SEIR model.

Fig. 1

Outbreak dynamics of COVID-19 across Europe and prediction of different exit strategies. The dots represent daily new cases. The brown and red curves illustrate the fit of the SEIR model and the effective reproduction number for the time period until May 10, 2020. The gray shaded area highlights the model predictions from May 10 until June 20, 2020. The dashed brown, orange, and red curves illustrate the projections for three possible exit strategies: a constant continuation at the effective reproduction number $R_{\mathrm{t}}$ from May 10, 2020, a gradual return to the basic reproduction number $R_0$ within three months, and a rapid to $R_0$ within one months

Fig. 2

Basic reproduction number $R_0$ of the COVID-19 outbreak across Europe. The basic reproduction number characterizes the initial number of new infectious created by one infectious individual. It has maximum values in Germany, the Netherlands, and Spain, with 6.33, 5.88, and 5.19 and minimum values in Bulgaria, Croatia, and Lithuania with 1.29, 0.93, and 0.91

Fig. 3

Effective reproduction number $R_{\mathrm{t}}$ of the COVID-19 outbreak across Europe. The effective reproduction number characterizes the current number of new infectious created by one infectious individual. It has maximum values in Sweden, Bulgaria, and Poland all with 1.01, 0.99, and 0.96 and minimum values in Lithuania, Hungary, and Slovakia with 0.41, 0.37, and 0.28 as of May 10, 2020

Fig. 4

Correlation between reduction in mobility and effective reproduction number of the COVID-19 outbreak across Europe. Purple, blue, grey, and black dots represent reduction in air traffic, driving, walking, and transit mobility; red curves show effective reproduction number R(t) with 95% confidence interval. The mean time delay $\mathrm{\Delta }t$ highlights the temporal delay between reduction in mobility and effective reproduction number. Spearman’s rank correlation $\rho$, measures of the statistical dependency between mobility and reproduction, and reveals the strongest correlation in the Netherlands, Germany, Ireland, Spain, and Sweden with 0.99 and 0.98

Fig. 5

Parameters of the COVID-19 outbreak across Europe. Basic reproduction number $R_0$, effective reproduction number $R_{\mathrm{t}}$, adaptation time $t^{\ast }$ and time delay $\mathrm{\Delta }t$. The adaptation time $t^{\ast }$ characterizes the time between the beginning of the outbreak and the reduction in the effective reproduction number; the time delay $\mathrm{\Delta }t$ characterizes the mean time between the reduction in air travel, driving, walking, and transit mobility and the reduction in the effective reproduction number

Fig. 6

Adaptation time $t^{\ast }$ between beginning of the outbreak and reduction of the effective reproduction number across Europe. The adaptation time characterizes the time between the beginning of the outbreak at 100 confirmed cases and the reduction in the effective reproduction number. It has maximum values in Bulgaria and Slovakia with 37.04 and 31.80 days and minimum values in Luxembourg and Slovenia with 5.77 and 5.64 days

Fig. 7

Time delay $\mathrm{\Delta }t$ between reduction of air travel and reduction of the effective reproduction number across Europe. The time delay characterizes the mean time between the reduction in air travel, driving, walking, and transit mobility and the reduction in the effective reproduction number. It has maximum values in Bulgaria and Slovakia with 43.00 and 40.25 days and minimum values in Germany and the Netherlands both with 3.25 and 0.75 days

Fig. 8

SEIR model with time-varying effective reproduction number. Increasing the basic reproduction number $R_0$ increases the initial growth, and with it the number of cases. The temporary equilibrium for the smaller basic reproduction number of $R_0=2.5$ is $s_{\infty }^{\ast }=0.948$ and $r_{\infty }^{\ast }=0.052$ and for the larger basic reproduction number of $R_0=5.0$ is $s_{\infty }^{\ast }=0.544$ and $r_{\infty }^{\ast }=0.456$. Latent period $A=2.5$ days, infectious period $C=6.5$ days, basic reproduction number $R_0=[5.0,4.5,4.0,3.5,3.0,2.5]$, effective reproduction number $R_{\mathrm{t}}=0.75$, adaptation time $t^{\ast }=20$ days, and transition time $T=15$ days

Fig. 9

SEIR model with time-varying effective reproduction number. Increasing the reproduction number $R_{\mathrm{t}}$ decreases the effect of interventions and increases the number of cases. The temporary equilibrium for the smaller effective reproduction number of $R_{\mathrm{t}}=0.4$ is $s_{\infty }^{\ast }=0.764$ and $r_{\infty }^{\ast }=0.236$ and for the larger effective reproduction number of $R_0=0.9$ is $s_{\infty }^{\ast }=0.594$ and $r_{\infty }^{\ast }=0.406$. Latent period $A=2.5$ days, infectious period $C=6.5$ days, basic reproduction number $R_0=4.5$, effective reproduction number $R_{\mathrm{t}}=[0.4,0.5,0.6,0.7,0.8,0.9]$, adaptation time $t^{\ast }=20$ days, and transition time $T=15$ days

Fig. 10

SEIR model with time-varying effective reproduction number. Increasing the adaptation time $t^{\ast }$ to interventions increases the time spent at a high reproduction number, and with it the number of cases. The temporary equilibrium for the faster adaptation of $t^{\ast }=10$ days is $s_{\infty }^{\ast }=0.956$ and $r_{\infty }^{\ast }=0.044$ and for the slower adaptation of $t^{\ast }=22$ days is $s_{\infty }^{\ast }=0.550$ and $r_{\infty }^{\ast }=0.450$. Latent period $A=2.5$ days, infectious period $C=6.5$ days, basic reproduction number $R_0=4.5$, effective reproduction number $R_{\mathrm{t}}=R_0/6=0.75$, adaptation time $t^{\ast }=[10,12,14,16,18,20,22]$ days, and transition time $T=15$ days

Fig. 11

Time-varying effective reproduction number R(t). Comparison of constant, hyperbolic tangent, and random walk type ansatz. The constant effective reproduction number predicts an exponential increase in the number of cases that fits the initial but not for the later stages of the COVID-19 outbreak, left. The hyperbolic tangent type reproduction number predicts a smooth early increase and later saturation of the number of cases, middle. The random walk type reproduction number predicts a daily varying, non-smooth early increase and later saturation of the number of cases, right. Dots represent reported cases; orange curves illustrate fit with 95% confidence interval; red curves shows effective reproduction number with 95% confidence interval; here illustrated for the case of Austria