Crossing complexity of space-filling curves reveals entanglement of S-phase DNA

Abstract

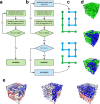
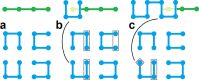
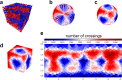
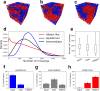
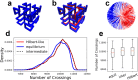
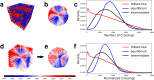
Space-filling curves have been used for decades to study the folding principles of globular proteins, compact polymers, and chromatin. Formally, space-filling curves trace a single circuit through a set of points (x,y,z); informally, they correspond to a polymer melt. Although not quite a melt, the folding principles of Human chromatin are likened to the Hilbert curve: a type of space-filling curve. Hilbert-like curves in general make biologically compelling models of chromatin; in particular, they lack knots which facilitates chromatin folding, unfolding, and easy access to genes. Knot complexity has been intensely studied with the aid of Alexander polynomials; however, the approach does not generalize well to cases of more than one chromosome. Crossing complexity is an understudied alternative better suited for quantifying entanglement between chromosomes. Do Hilbert-like configurations limit crossing complexity between chromosomes? How does crossing complexity for Hilbert-like configurations compare to equilibrium configurations? To address these questions, we extend the Mansfield algorithm to enable sampling of Hilbert-like space filling curves on a simple cubic lattice. We use the extended algorithm to generate equilibrium, intermediate, and Hilbert-like configurational ensembles and compute crossing complexity between curves (chromosomes) in each configurational snapshot. Our main results are twofold: (a) Hilbert-like configurations limit entanglement between chromosomes and (b) Hilbert-like configurations do not limit entanglement in a model of S-phase DNA. Our second result is particularly surprising yet easily rationalized with a geometric argument. We explore ergodicity of the extended algorithm and discuss our results in the context of more sophisticated models of chromatin.

Fig 1. Algorithm for generating multiple lattice Space Filling Curves (SFC) on a simple cubic lattice.

a, Mansfield algorithm for generating single lattice SFCs. b, Mansfield algorithm for generating multiple lattice SFCs with algorithmic insertions in blue. c, Schematic of the end-attack chain rearrangement maneuver. d, Configurational snapshots of one, two, and three SFCs on a simple cubic lattice, respectively. e, Configurational snapshots of equilibrium, intermediate, and Hilbert-like SFCs on a cubic lattice, respectively. Each lattice has one chain; blue to red colormap emphasizes differences in scaling. Configurations are generated with novel steps that partially control chain end-to-end scaling (see methods).

Fig 2. Computational details of nest and replace chain rearrangements.

Monomers in the green lattice SFC (top left) are replaced sequentially–from end to end–by configurational snapshots of 2x2 lattice SFCs (blue). a, Begin by exhaustively computing all 2x2 lattice SFCs. b, End-wall orientation of valid replacement paths (grey boxes) must match the bond orientation of the monomer (to be replaced) and its neighbor (next to be replaced). c, Start point of valid replacement paths must be adjacent to the endpoint of the previous replacement (grey diamond). Valid replacements are selected at random. Iterative steps (b) and (c) are repeated for all monomers. The procedure is trivial to generalize for three dimensions.

Fig 3. Crossing complexity for two curves on a simple cubic lattice.

a, Two SFCs on a simple 16x16x16 cubic lattice. b, Putative translations are applied over a set of test directions that evenly cover the space S² (spherical surface); chain crossings are enumerated and color coded for each direction. c, Enumerated chain crossings mapped onto the unit sphere. d, Enumerated chain crossings mapped onto the unit cube. e, Mercator projection of chain crossings.

Fig 4. Crossing complexity for two Lattice space filling curves on a simple cubic lattice.

a-c, Configurational snapshots of equilibrium, intermediate, and Hilbert-like curves, respectively. d-e, The distribution of crossing complexity enumerated for 1000 test directions in ensembles of equilibrium, intermediate, and Hilbert-like curves. Average crossing complexity is lowest for Hilbert-like curves. f-h, Crossing complexity partially distinguishes between snapshots of each ensemble. We used a Kolmogorov-Smirnov test to classify snapshots in each ensemble. In each case most of the snapshots classify into the correct ensemble (details in methods).

Fig 5. High crossing complexity in a lattice Space Filling Curve (SFC) model of S-phase DNA.

a, Begin with a single lattice SFC; we consider equilibrium, intermediate, and Hilbert-like configurations. b, Replicate the Lattice SFC in place akin to S-phase DNA; the red and blue curves (chromosomes) remain juxtaposed in in register. c, Compute the crossing complexity by enumerating chain crossings over a set of test directions that evenly cover the space S². d, Distribution of enumerated chain crossings for each ensemble. e, Average number of chain crossings is lowest in the equilibrium ensemble and comparable in the intermediate and Hilbert-like ensembles.

Fig 6. A simple geometric argument suggests that doubled space-filling curves produce the same distribution of enumerated chain crossings regardless of folding principles.

a, Space filling curve on a 4x4x4 lattice. b-e, Four layers of the space filling curve projected along one axis. f, A doubled 4x4x4 space filling curve. g-j, A single segment of the doubled curve followed through each layer of the blue curve. Chain crossings occur in panels g and j.

Fig 7. Statistics of lattice space filling curves suggest they are ergodic.

Top row, Results for equilibrium configurations. Bottom row, Results for Hilbert-like configurations. a and d, Probability for chain ends at each lattice site are distributed around the expected value: inverse of the lattice size (n). b and e, Distribution of total chain torsion (measured with the triple product) has zero mean. c and f, Bonds for each chain have equal probability of alignment along the x, y, and z axes. These findings suggest–but do not prove–that configurations are sampled without bias.

Fig 8. Schematic of four types of chain rearrangement maneuvers.

a, End attack is an intermolecular chain rearrangement in which a bond is broken and annealed to the end of a different chain. b, Backbite is an intramolecular chain rearrangement in which a bond is broken and annealed to the end of the same chain. c, Bond flip is an intermolecular chain rearrangement in which two parallel bonds are broken and reformed in perpendicular orientation. d, Nest and replace is a rearrangement in which a single monomer is replaced by an entire configurational snapshot.

Fig 9. Crossing complexity visualized for the simple case of two line segments.

a, Two curves shown in red and blue. b, Putative translations are applied over a set of test directions that evenly cover the space S² (spherical surface); chain crossings are enumerated and color coded for each direction. c, Enumerated chain crossings mapped onto the unit sphere.

Fig 10. A key result of this work is robust to crossing complexity normalization.

a, Snapshot of two space filling curves on a lattice. b, Chain crossings enumerated for a set of test directions. c, The distribution of chain crossings over three different ensembles of configurational snapshots: distributions differ for equilibrium, intermediate and Hilbert-like curves. d, Chain crossings enumerated for a set of test directions and weighed by the lattice size measured in the direction of each separation path. e, Chain crossings normalized by weight. f, Results are robust to crossing complexity normalization.