Integrating genotypes and phenotypes improves long-term forecasts of seasonal influenza A/H3N2 evolution
- PMID: 32876050
- PMCID: PMC7553778
- DOI: 10.7554/eLife.60067
Integrating genotypes and phenotypes improves long-term forecasts of seasonal influenza A/H3N2 evolution
Abstract
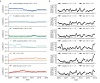
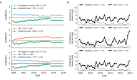
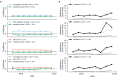
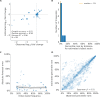
Seasonal influenza virus A/H3N2 is a major cause of death globally. Vaccination remains the most effective preventative. Rapid mutation of hemagglutinin allows viruses to escape adaptive immunity. This antigenic drift necessitates regular vaccine updates. Effective vaccine strains need to represent H3N2 populations circulating one year after strain selection. Experts select strains based on experimental measurements of antigenic drift and predictions made by models from hemagglutinin sequences. We developed a novel influenza forecasting framework that integrates phenotypic measures of antigenic drift and functional constraint with previously published sequence-only fitness estimates. Forecasts informed by phenotypic measures of antigenic drift consistently outperformed previous sequence-only estimates, while sequence-only estimates of functional constraint surpassed more comprehensive experimentally-informed estimates. Importantly, the best models integrated estimates of both functional constraint and either antigenic drift phenotypes or recent population growth.
Keywords: antigenic drift; evolution; evolutionary biology; infectious disease; influenza; microbiology; phenotypes; prediction; virus.
Plain language summary
Vaccination is the best protection against seasonal flu. It teaches the immune system what the flu virus looks like, preparing it to fight off an infection. But the flu virus changes its molecular appearance every year, escaping the immune defences learnt the year before. So, every year, the vaccine needs updating. Since it takes almost a year to design and make a new flu vaccine, researchers need to be able to predict what flu viruses will look like in the future. Currently, this prediction relies on experiments that assess the molecular appearance of flu viruses, a complex and slow approach. One alternative is to examine the virus's genetic code. Mathematical models try to predict which genetic changes might alter the appearance of a flu virus, saving the cost of performing specialised experiments. Recent research has shown that these models can make good predictions, but including experimental measures of the virus’ appearance could improve them even further. This could help the model to work out which genetic changes are likely to be beneficial to the virus, and which are not. To find out whether experimental data improves model predictions, Huddleston et al. designed a new forecasting tool which used 25 years of historical data from past flu seasons. Each forecast predicted what the virus population might look like the next year using the previous year's genetic code, experimental data, or both. Huddleston et al. then compared the predictions with the historical data to find the most useful data types. This showed that the best predictions combined changes from the virus's genetic code with experimental measures of its appearance. This new forecasting tool is open source, allowing teams across the world to start using it to improve their predictions straight away. Seasonal flu infects between 5 and 15% of the world's population every year, causing between quarter of a million and half a million deaths. Better predictions could lead to better flu vaccines and fewer illnesses and deaths.
Conflict of interest statement
JH, JB, TR, XX, RK, DW, LW, BE, RD, JM, SF, KN, NK, SW, HH, IB, KS, PB, RN, TB No competing interests declared
Figures
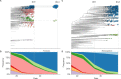
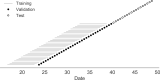

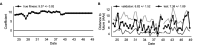
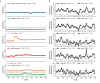
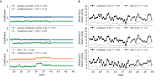
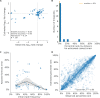

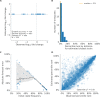
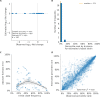


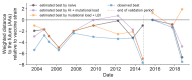

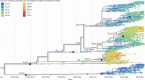


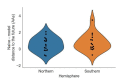
Comment in
-
The challenges of vaccine strain selection.Elife. 2020 Oct 13;9:e62955. doi: 10.7554/eLife.62955. Elife. 2020. PMID: 33048046 Free PMC article.
References
-
- Bedford T, Riley S, Barr IG, Broor S, Chadha M, Cox NJ, Daniels RS, Gunasekaran CP, Hurt AC, Kelso A, Klimov A, Lewis NS, Li X, McCauley JW, Odagiri T, Potdar V, Rambaut A, Shu Y, Skepner E, Smith DJ, Suchard MA, Tashiro M, Wang D, Xu X, Lemey P, Russell CA. Global circulation patterns of seasonal influenza viruses vary with antigenic drift. Nature. 2015;523:217–220. doi: 10.1038/nature14460. - DOI - PMC - PubMed
-
- Belongia EA, Simpson MD, King JP, Sundaram ME, Kelley NS, Osterholm MT, McLean HQ. Variable influenza vaccine effectiveness by subtype: a systematic review and meta-analysis of test-negative design studies. The Lancet Infectious Diseases. 2016;16:942–951. doi: 10.1016/S1473-3099(16)00129-8. - DOI - PubMed
-
- Bradski G. The OpenCV Library. 4.3.0Dr Dobb’s Journal of Software Tools. 2000 https://opencv.org/
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Miscellaneous

