A comparison of dominance rank metrics reveals multiple competitive landscapes in an animal society

Abstract

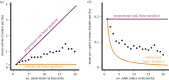
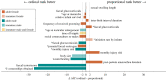
Across group-living animals, linear dominance hierarchies lead to disparities in access to resources, health outcomes and reproductive performance. Studies of how dominance rank predicts these traits typically employ one of several dominance rank metrics without examining the assumptions each metric makes about its underlying competitive processes. Here, we compare the ability of two dominance rank metrics-simple ordinal rank and proportional or 'standardized' rank-to predict 20 traits in a wild baboon population in Amboseli, Kenya. We propose that simple ordinal rank best predicts traits when competition is density-dependent, whereas proportional rank best predicts traits when competition is density-independent. We found that for 75% of traits (15/20), one rank metric performed better than the other. Strikingly, all male traits were best predicted by simple ordinal rank, whereas female traits were evenly split between proportional and simple ordinal rank. Hence, male and female traits are shaped by different competitive processes: males are largely driven by density-dependent resource access (e.g. access to oestrous females), whereas females are shaped by both density-independent (e.g. distributed food resources) and density-dependent resource access. This method of comparing how different rank metrics predict traits can be used to distinguish between different competitive processes operating in animal societies.

Keywords: baboons; longitudinal studies; proportional rank; relative rank; social dominance; standardized rank.

Figure 1.

Differences between proportional and simple ordinal rank in two differently sized hierarchies. Ranks with darker shading have a competitive advantage over those with lighter shading. The fifth-ranking individual in each hierarchy is demarcated with a white border. Under a simple ordinal rank framework, being ranked fifth confers the same competitive advantages independent of hierarchy size. Under a proportional rank framework, being ranked fifth is more advantageous in a hierarchy of 9 (proportional rank = 0.5) than in a hierarchy of 5 (proportional rank = 0). Adapted from Levy et al. [33].

Figure 2.

(a) The theoretical and empirical relationships between male hierarchy size (x-axis) and resource availability (y-axis) using the example of oestrous female baboons, a resource over which male baboons compete for mating success. The orange line shows a theoretical scenario in which the number of oestrous females in the group (total resource base) is constant as the number of males in the hierarchy increases; in this case, male mating success (the resulting measured trait) would be predicted by simple ordinal rank. The purple line shows a scenario in which the number of oestrous females increases in proportion to the number of males in the hierarchy; in this case, male mating success would be predicted by proportional rank. The slope of the orange line is 0 and the intercept is r₁, which designates the quantity of resources available in a hierarchy size of 1 male (r₁ = 0.2 oestrous females in this figure). This value, r₁, determines the slope of the purple line; i.e. for proportional rank to perfectly predict mating success, resource availability must increase by r₁, the quantity available to the first male, as each male is added to the hierarchy. The empirical relationship between male hierarchy size and the number of oestrous females (Amboseli baboon data; black points) is positive, but the slope is closer to the orange line than the purple line. Thus, we expect simple ordinal rank to best predict mating success. (b) Similar to (a), but the number of oestrous females is plotted per capita (i.e. per adult male in the hierarchy). The orange curve illustrates the case in which the resource stays constant across different hierarchy sizes; thus, average per capita resource access declines as hierarchy size increases. The purple line illustrates the case in which the resource base increases proportionately with hierarchy size; thus, average per capita resource access is fixed. The black points represent the same empirical data as in (a). Note that the framework above assumes that any given individual's ability to maintain control of a resource is independent of group size. (Online version in colour.)

Figure 3.

Visualization of model outcomes when predicting the same trait with simple ordinal rank (labelled ‘ordinal rank’) versus proportional rank. Each bar corresponds to a trait, and its value corresponds to a difference in AIC scores between models that used simple ordinal versus proportional rank. Vertical dashed lines represent |ΔAIC| = 2. For traits whose bars are within the dashed lines, neither rank metric performed substantially better than the other (5/20 analyses; we did not find any indication that the ability of the models to differentiate between the predictive power of simple ordinal versus proportional rank depended on the duration of the study; p = 0.9, Pearson's product moment correlation). For traits whose bars are to the left of the dashed lines, simple ordinal rank was a better predictor of the trait than proportional rank (11/20), and vice versa for traits whose bars are to the right of the dashed lines (4/20). Colours of bars indicate sex (male, female and both), and shading indicates age class (adult or maternal rank of immatures). Asterisks indicate the seven traits for which only one rank metric predicted the trait better than the null model. The top two bars, sexual swelling length and faecal glucocorticoids, were traits measured in adult females and immature males, respectively. See electronic supplementary material, table S1 for information about the originally identified rank effects. (Online version in colour.)