A Faster and More Accurate Algorithm for Calculating Population Genetics Statistics Requiring Sums of Stirling Numbers of the First Kind

Abstract

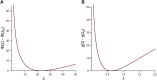
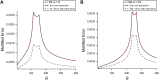
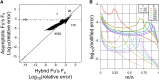
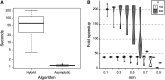
Ewen's sampling formula is a foundational theoretical result that connects probability and number theory with molecular genetics and molecular evolution; it was the analytical result required for testing the neutral theory of evolution, and has since been directly or indirectly utilized in a number of population genetics statistics. Ewen's sampling formula, in turn, is deeply connected to Stirling numbers of the first kind. Here, we explore the cumulative distribution function of these Stirling numbers, which enables a single direct estimate of the sum, using representations in terms of the incomplete beta function. This estimator enables an improved method for calculating an asymptotic estimate for one useful statistic, Fu's [Formula: see text] By reducing the calculation from a sum of terms involving Stirling numbers to a single estimate, we simultaneously improve accuracy and dramatically increase speed.

Keywords: Asymptotic analysis; Cumulative distribution functions; Evolutionary inference; Numerical algorithms; Population genetics statistics; Stirling numbers of the first kind.

Figure 1

Graphs of $\phi \left(z\right)-\phi \left(z_0\right)$ (A) and $\chi \left(t\right)-\chi \left(t_0\right)$ (B) for $n=100$, $m=38$, with $z_0\hspace{0.17em}\doteq \hspace{0.17em}22.81$ and $t_0=\frac{19}{31}\hspace{0.17em}\doteq \hspace{0.17em}0.61$.

Figure 2

Mollified error in estimating Fu’s $F_s$ for $\theta \in \left(10,400\right)$, $m=75$ and $n=100$ (A) and for $m=275$ and $n=500$ (B). The data for the dashed curves are multiplied by a factor of 10 (A) and 100 (B), to make the error curves visible in the figures. Refer to the text for further details.

Figure 3

(A) Comparison of relative error of the estimator from (Chen 2019) and the single term asymptotic estimator in (35). Relative error for each is calculated against the arbitrary precision implementation described in (Chen 2019). In total, 10,000 calculations were performed with n randomly sampled from a uniform distribution between 50 and 500; m between 2 and n; and θ between 1 and 50. A solid diagonal line is drawn at $y=x$. Dotted lines are drawn at a relative error of 0.001. Numbers within each quadrant defined by the dotted lines indicate the number of points in each quadrant. The red dot indicates the one case where the relative error was $>0.001$ and the error of (35) was greater than the estimator from (Chen 2019). (B) Comparison of mollified error (34) as a function of m. For this plot, we fixed $n=100$ (solid lines) or 500 (dotted lines) and $\theta \in \left(10,500\right)$ (as indicated by different line colors).

Figure 4

(A) Comparison of run times between the hybrid algorithm from (Chen 2019) and the single term asymptotic estimator in (35). 100 iterations were run, each with 10,000 calculations; the time elapsed for each set of 10,000 calculations was recorded and plotted here. The same set of parameters were used for each algorithm. The order of running the algorithms was alternated with each iteration. The dark horizontal line indicates the median, the box indicates the first and third quartiles, the whiskers are drawn at 1.5x the interquartile range, and outliers are represented by open circles. The median for the hybrid algorithm is 62.64 s; the median for the asymptotic algorithm is 1.17 s. (B) Detailed benchmarking for $n=100$ (open violins) or 500 (gray violins), $m\in \left(0.1n,0.2n,\dots ,0.9n\right)$, and $\theta \in \left(10,500\right)$. Fold speedup (ratio of the time taken for the hybrid calculator to that taken for the aysmptotic estimator) is plotted on the y-axis. Each dot represents one set of parameters; the violin plots summarize the density of points on the y-axis. Times were calculated for 100 iterations of each estimator for the same parameter values.