A Guard Cell Abscisic Acid (ABA) Network Model That Captures the Stomatal Resting State
- PMID: 32903539
- PMCID: PMC7438572
- DOI: 10.3389/fphys.2020.00927
A Guard Cell Abscisic Acid (ABA) Network Model That Captures the Stomatal Resting State
Abstract
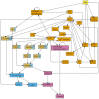
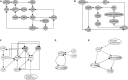
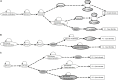
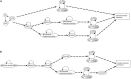
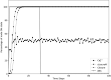
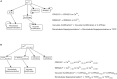
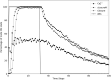
Stomatal pores play a central role in the control of carbon assimilation and plant water status. The guard cell pair that borders each pore integrates information from environmental and endogenous signals and accordingly swells or deflates, thereby increasing or decreasing the stomatal aperture. Prior research shows that there is a complex cellular network underlying this process. We have previously constructed a signal transduction network and a Boolean dynamic model describing stomatal closure in response to signals including the plant hormone abscisic acid (ABA), calcium or reactive oxygen species (ROS). Here, we improve the Boolean network model such that it captures the biologically expected response of the guard cell in the absence or following the removal of a closure-inducing signal such as ABA or external Ca2+. The expectation from the biological system is reversibility, i.e., the stomata should reopen after the closing signal is removed. We find that the model's reversibility is obstructed by the previously assumed persistent activity of four nodes. By introducing time-dependent Boolean functions for these nodes, the model recapitulates stomatal reopening following the removal of a signal. The previous version of the model predicts ∼20% closure in the absence of any signal due to uncertainty regarding the initial conditions of multiple network nodes. We systematically test and adjust these initial conditions to find the minimally restrictive combinations that appropriately result in open stomata in the absence of a closure signal. We support these results by an analysis of the successive stabilization of feedback motifs in the network, illuminating the system's dynamic progression toward the open or closed stomata state. This analysis particularly highlights the role of cytosolic calcium oscillations in causing and maintaining stomatal closure. Overall, we illustrate the strength of the Boolean network modeling framework to efficiently capture cellular phenotypes as emergent outcomes of intracellular biological processes.
Keywords: Boolean model; Boolean network; guard cell; memory; signal transduction; stomatal closure.
Copyright © 2020 Maheshwari, Assmann and Albert.
Figures
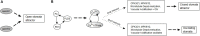
Similar articles
-
A network-based modeling framework reveals the core signal transduction network underlying high carbon dioxide-induced stomatal closure in guard cells.PLoS Biol. 2024 May 1;22(5):e3002592. doi: 10.1371/journal.pbio.3002592. eCollection 2024 May. PLoS Biol. 2024. PMID: 38691548 Free PMC article.
-
Signaling Transduction of ABA, ROS, and Ca2+ in Plant Stomatal Closure in Response to Drought.Int J Mol Sci. 2022 Nov 26;23(23):14824. doi: 10.3390/ijms232314824. Int J Mol Sci. 2022. PMID: 36499153 Free PMC article. Review.
-
Predicting essential components of signal transduction networks: a dynamic model of guard cell abscisic acid signaling.PLoS Biol. 2006 Oct;4(10):e312. doi: 10.1371/journal.pbio.0040312. PLoS Biol. 2006. PMID: 16968132 Free PMC article.
-
A new discrete dynamic model of ABA-induced stomatal closure predicts key feedback loops.PLoS Biol. 2017 Sep 22;15(9):e2003451. doi: 10.1371/journal.pbio.2003451. eCollection 2017 Sep. PLoS Biol. 2017. Update in: PLoS Biol. 2024 May 1;22(5):e3002592. doi: 10.1371/journal.pbio.3002592. PMID: 28937978 Free PMC article. Updated.
-
Abscisic Acid-Induced Stomatal Closure: An Important Component of Plant Defense Against Abiotic and Biotic Stress.Front Plant Sci. 2021 Mar 4;12:615114. doi: 10.3389/fpls.2021.615114. eCollection 2021. Front Plant Sci. 2021. PMID: 33746999 Free PMC article. Review.
Cited by
-
Inference of a Boolean Network From Causal Logic Implications.Front Genet. 2022 Jun 16;13:836856. doi: 10.3389/fgene.2022.836856. eCollection 2022. Front Genet. 2022. PMID: 35783282 Free PMC article.
-
Signatures of natural selection in a foundation tree along Mediterranean climatic gradients.Mol Ecol. 2022 Mar;31(6):1735-1752. doi: 10.1111/mec.16351. Epub 2022 Jan 27. Mol Ecol. 2022. PMID: 35038378 Free PMC article.
-
Deep dive into CO2-dependent molecular mechanisms driving stomatal responses in plants.Plant Physiol. 2021 Dec 4;187(4):2032-2042. doi: 10.1093/plphys/kiab342. Plant Physiol. 2021. PMID: 35142859 Free PMC article.
-
HHIP's Dynamic Role in Epithelial Wound Healing Reveals a Potential Mechanism of COPD Susceptibility.bioRxiv [Preprint]. 2024 Oct 8:2024.09.05.611545. doi: 10.1101/2024.09.05.611545. bioRxiv. 2024. PMID: 39416045 Free PMC article. Preprint.
-
Optogenetic control of the guard cell membrane potential and stomatal movement by the light-gated anion channel GtACR1.Sci Adv. 2021 Jul 9;7(28):eabg4619. doi: 10.1126/sciadv.abg4619. Print 2021 Jul. Sci Adv. 2021. PMID: 34244145 Free PMC article.
References
LinkOut - more resources
Full Text Sources
Miscellaneous

