Deconstructing laws of accessibility and facility distribution in cities

Abstract

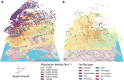
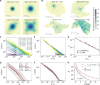
The era of the automobile has seriously degraded the quality of urban life through costly travel and visible environmental effects. A new urban planning paradigm must be at the heart of our road map for the years to come, the one where, within minutes, inhabitants can access their basic living needs by bike or by foot. In this work, we present novel insights of the interplay between the distributions of facilities and population that maximize accessibility over the existing road networks. Results in six cities reveal that travel costs could be reduced in half through redistributing facilities. In the optimal scenario, the average travel distance can be modeled as a functional form of the number of facilities and the population density. As an application of this finding, it is possible to estimate the number of facilities needed for reaching a desired average travel distance given the population distribution in a city.

Fig. 1. Illustration of the three datasets.

(A) Datasets in NYC. The lower layer depicts the map and road networks of the city. The middle and upper layers illustrate the population density and the locations of the 10 selected types of facilities in the same region, respectively. (B) Datasets in Doha. Compared with very dense NYC, Doha has a simpler road network, less population, and sparser facilities. Illustration of the three datasets in NYC (A) and Doha (B). The lower layer depicts the map and road networks of the city. The middle and upper layers illustrate the population density and the locations of the 10 selected types of facilities in the same region, respectively. Compared with very dense NYC, Doha has a simpler road network, less population, and sparser facilities.

Fig. 2. Service communities of hospitals in the actual and optimal scenarios in Boston and gain of travel distance per block.

(A) Service communities of the hospitals, as measured from empirical data in Boston. The dots refer to the blocks in the city. The color indicates the population in each community. (B) Service communities of the optimally distributed hospitals in Boston. In this optimal scenario, both of the area and the population of communities are generally more equable than those in the actual scenario. (C) The block gain index r_i in logarithmic scale in Boston. The blocks in green indicate that the residents are better served in reality; r_i does not have units. The blocks in red indicate that their actual travel distance to the hospital is larger than the optimal distance and they are underserved, such as in the northern and southeastern areas.

Fig. 3. Optimality of planning by facility type and city.

(A) The average travel distance in actual scenario, $\widehat{L}$, and optimal scenario, L, for the 10 types of facilities in the six cities. (B) $\widehat{L}$ as a function of D_occ, the ratio between N and N_occ, in the six cities. The dot refers to one of the 10 types of facilities in a given city. Cities display different descending rates. (C) L as a function of D_occ in the six cities. All cities show similar descending rates. (D) Box plot of the optimality index, R, by facility type. Facility types are ranked by their average densities in the six cities in the descending order. Among the facility types, fire station is the most optimally distributed and bank and school are the worst. In general, facility type with lower density is better located than dense facility type from the perspective of collective benefit maximization.

Fig. 4. Fitted power law for the distribution of hospitals per city.

(A) Actual hospital density (inverse of the area of community) versus population density at service community level. Each colored dot refers to a service community and the size represents its population, as shown in Fig. 2A. The full line represents the best fitted power law. The colored shadow represents the 95% confidence interval. The low r² indicates that a clear power law can not be found and the fitted exponent differs from the empirically observed 2/3 at larger scales (18). (B) Hospital density versus population density in the optimal scenario. The full lines show clear power laws, with exponents close to 2/3 in all cities. The r² values are higher and confidence intervals are narrower than the actual scenario. The fitted exponents for other facility types are numerically provided in table S1. (C) Change of fitted exponent β with D_occ in the optimal scenario in the six cities. Each β is calculated by optimally distributing a given number of facilities in the city. The gray dashed and full lines indicate that β = 2/3 and D_occ = 0.2, respectively. (D) Change of fitted exponent β with D_occ in the optimal scenario in four toy cities.

Fig. 5. Modeling of optimal travel distance to facilities in toy and real-world cities.

(A) Population distributions of four selected toy cities. (B) Population distributions of four selected real-world cities, among which Paris is the most centralized and Melbourne is the most polycentric. (C and D) Simulated and modeled optimal travel distance, L, versus the number of facilities, N, in toy cities and real-world cities, respectively. The dots represent the simulated L with varying N. The lines represent the fitted model L(N) in Eq. 5. Cities are ranked by urban centrality (UCI) in the descending order in the legend. (E) Simulated and modeled L versus αN in toy cities. By scaling N with α, we collapse the curves of L with UCI lower than 0.9 into a single one. (F) Simulated and modeled L versus αN in real-world cities. The black line represents the function in Eq. 6, approached by the simulated L in all cities. (G) Relation between α and N_occ. α can be well fitted with N_occ, suggesting that the decay rate of shared population in blocks without facilities is in inverse proportion to the urban area in one city for a small N. (H) Validation of the universal function in LA and Barcelona.