Autoreservoir computing for multistep ahead prediction based on the spatiotemporal information transformation
- PMID: 32917894
- PMCID: PMC7486927
- DOI: 10.1038/s41467-020-18381-0
Autoreservoir computing for multistep ahead prediction based on the spatiotemporal information transformation
Abstract
We develop an auto-reservoir computing framework, Auto-Reservoir Neural Network (ARNN), to efficiently and accurately make multi-step-ahead predictions based on a short-term high-dimensional time series. Different from traditional reservoir computing whose reservoir is an external dynamical system irrelevant to the target system, ARNN directly transforms the observed high-dimensional dynamics as its reservoir, which maps the high-dimensional/spatial data to the future temporal values of a target variable based on our spatiotemporal information (STI) transformation. Thus, the multi-step prediction of the target variable is achieved in an accurate and computationally efficient manner. ARNN is successfully applied to both representative models and real-world datasets, all of which show satisfactory performance in the multi-step-ahead prediction, even when the data are perturbed by noise and when the system is time-varying. Actually, such ARNN transformation equivalently expands the sample size and thus has great potential in practical applications in artificial intelligence and machine learning.
Conflict of interest statement
The authors declare no competing interests.
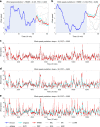
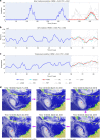
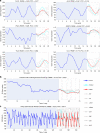
Figures



References
-
- Thombs LA, Schucany WR. Bootstrap prediction intervals for autoregression. J. Am. Stat. Assoc. 1990;85:486–492.
-
- Box GEP, Pierce DA. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. J. Am. Stat. Assoc. 1970;65:1509–1526.
-
- Jiang J, Lai YC. Model-free prediction of spatiotemporal dynamical systems with recurrent neural networks: Role of network spectral radius. Phys. Rev. Res. 2019;1:033056.
-
- Schmidhuber J, Hochreiter S. Long short-term memory. Neural Comput. 1997;9:1735–1780. - PubMed
-
- Alahi, A. et al. Social lstm: human trajectory prediction in crowded spaces. in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 961–971 (2016).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

