Global dynamics of a multi-strain SEIR epidemic model with general incidence rates: application to COVID-19 pandemic

Abstract

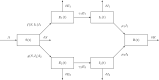
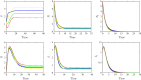
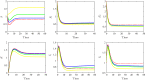
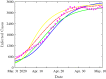
This paper investigates the global stability analysis of two-strain epidemic model with two general incidence rates. The problem is modelled by a system of six nonlinear ordinary differential equations describing the evolution of susceptible, exposed, infected and removed individuals. The wellposedness of the suggested model is established in terms of existence, positivity and boundedness of solutions. Four equilibrium points are given, namely the disease-free equilibrium, the endemic equilibrium with respect to strain 1, the endemic equilibrium with respect to strain 2, and the last endemic equilibrium with respect to both strains. By constructing suitable Lyapunov functional, the global stability of the disease-free equilibrium is proved depending on the basic reproduction number $R_0$ . Furthermore, using other appropriate Lyapunov functionals, the global stability results of the endemic equilibria are established depending on the strain 1 reproduction number $R_0^1$ and the strain 2 reproduction number $R_0^2$ . Numerical simulations are performed in order to confirm the different theoretical results. It was observed that the model with a generalized incidence functions encompasses a large number of models with classical incidence functions and it gives a significant wide view about the equilibria stability. Numerical comparison between the model results and COVID-19 clinical data was conducted. Good fit of the model to the real clinical data was remarked. The impact of the quarantine strategy on controlling the infection spread is discussed. The generalization of the problem to a more complex compartmental model is illustrated at the end of this paper.

Keywords: Basic reproduction number; COVID-19; General incidence function; Global stability analysis; Multi-strain epidemic model; SEIR.

Fig. 1

Flowchart of two-strain SEIR model

Fig. 2

Time evolution of susceptible (top left), the strain 1 latent individuals (top middle), the strain 2 latent individuals (top right), the recovered (bottom left), the strain 1 infectious individuals (bottom middle) and the strain 2 infectious individuals (bottom right) illustrating the stability of the disease-free equilibrium ${\mathcal{E}}_f$. The bilinear incidence functions (dotted red), Beddington–DeAngelis incidence functions (yellow), Crowley–Martin incidence functions (green) and the non-monotone incidence functions (blue). (Color figure online)

Fig. 3

Time evolution of susceptible (top left), the strain 1 latent individuals (top middle), the strain 2 latent individuals (top right), the recovered (bottom left), the strain 1 infectious individuals (bottom middle) and the strain 2 infectious individuals (bottom right) illustrating the stability of the strain 1 endemic equilibrium ${\mathcal{E}}_{s_1}$. The bilinear incidence functions (dotted red), Beddington–DeAngelis incidence functions (yellow), Crowley–Martin incidence functions (green) and the non-monotone incidence functions (blue). (Color figure online)

Fig. 4

Time evolution of susceptible (top left), the strain 1 latent individuals (top middle), the strain 2 latent individuals (top right), the recovered (bottom left), the strain 1 infectious individuals (bottom middle) and the strain 2 infectious individuals (bottom right) illustrating the stability of the strain 2 endemic equilibrium ${\mathcal{E}}_{s_2}$. The bilinear incidence functions (dotted red), Beddington–DeAngelis incidence functions (yellow), Crowley–Martin incidence functions (green) and the non-monotone incidence functions (blue). (Color figure online)

Fig. 5

Time evolution of susceptible (top left), the strain 1 latent individuals (top middle), the strain 2 latent individuals (top right), the recovered (bottom left), the strain 1 infectious individuals (bottom middle) and the strain 2 infectious individuals (bottom right) illustrating the stability of the endemic equilibrium ${\mathcal{E}}_t$. The bilinear incidence functions (dotted red), Beddington–DeAngelis incidence functions (yellow), Crowley–Martin incidence functions (green) and the non-monotone incidence functions (blue). (Color figure online)

Fig. 6

Time evolution of infected cases with the bilinear incidence functions (dotted red), Beddington–DeAngelis incidence functions (yellow), Crowley–Martin incidence functions (green) and the non-monotone incidence functions (blue). The clinical infected cases are illustrated by magenta circles. (Color figure online)

Fig. 7

Time evolution of infected cases with the bilinear incidence functions (dotted red), Beddington–DeAngelis incidence functions (yellow), Crowley–Martin incidence functions (green) and the non-monotone incidence functions (blue). The clinical infected cases are illustrated by magenta circles. (Color figure online)

Fig. 8

Effect of quarantine strategy on the SEIR model dynamics