Dynamics of fluid displacement in mixed-wet porous media

Abstract

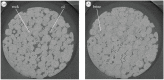
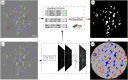
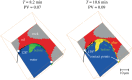
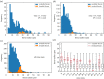
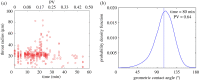
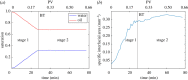
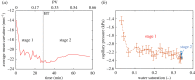
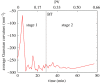
We identify a distinct two-phase flow invasion pattern in a mixed-wet porous medium. Time-resolved high-resolution synchrotron X-ray imaging is used to study the invasion of water through a small rock sample filled with oil, characterized by a wide non-uniform distribution of local contact angles both above and below 90^°. The water advances in a connected front, but throats are not invaded in decreasing order of size, as predicted by invasion percolation theory for uniformly hydrophobic systems. Instead, we observe pinning of the three-phase contact between the fluids and the solid, manifested as contact angle hysteresis, which prevents snap-off and interface retraction. In the absence of viscous dissipation, we use an energy balance to find an effective, thermodynamic, contact angle for displacement and show that this angle increases during the displacement. Displacement occurs when the local contact angles overcome the advancing contact angles at a pinned interface: it is wettability which controls the filling sequence. The product of the principal interfacial curvatures, the Gaussian curvature, is negative, implying well-connected phases which is consistent with pinning at the contact line while providing a topological explanation for the high displacement efficiencies in mixed-wet media.

Keywords: X-ray imaging; contact angle; mixed-wet; multiphase flow; porous media; wettability.

Figure 1.

2D slices of the 3D tomograms as they appear after reconstruction. (a) A slice of the image before water injection, while the image in (b) was taken at the end of water injection.

Figure 2.

Workflow for image segmentation. The images before water injection (figure 1a) were subtracted from the images with water (figure 1b). The resulting differential image is shown in (c) of this image: brighter areas correspond to the places invaded by water. We created a training dataset with manual classification of invaded voxels (green in a) versus non invaded by water (red). The machine learning WEKA algorithm computes image features (mean and variance) from the differential image, and these are given as input, together with the training dataset, to the random forest algorithm. The result is a classifier. We applied this classifier to the differential images obtained at each time step and obtained (b) binary images with 1 (white) where water invaded the sample and 0 (black) elsewhere. Combining these with the dry segmented image of the rock, we obtained the final three-phase images (d). In (d), grey is rock, red is oil and blue is water. (Online version in colour.)

Figure 3.

Top row: 3D rendering of rock (grey), oil (semi-transparent red) and water (blue) during waterflooding in the mixed-wet rock, at four time steps. Bottom row: Relation between the dimension of the throats and the phase occupying their centre at four times, during water invasion. Throats of a wide range of radii are invaded over time, showing that throat size is not the main parameter controlling filling. We started to count time since the onset of water invasion in the imaged domain. Pore volumes (PV) were computed considering the total volume of macro pores of the whole sample. (Online version in colour.)

Figure 4.

Visualization of a detail of the pore space where we can observe the pinning of the oil–water interface. During water injection, while the three-phase contact points (white dots) did not move, the interface changed its shape (from green to yellow), with a consequent increase in contact angle. Pore volumes (PV) were computed considering the total volume of macro pores of the whole sample. (Online version in colour.)

Figure 5.

(a–c) At each time step, we identified the throats available for invasion (connected to the water front) and compared these with the ones which were actually invaded. (d) Box-plot of available and invaded throats at each time step. (Online version in colour.)

Figure 6.

(a) Scatterplot where the radius of invaded throats is the dependent variable and the time at which they were filled is the dependent variable. (b) Geometric contact angle between water and oil on the high-quality image taken the end of waterflooding. The vertical line shows the average contact angle (109^°). (Online version in colour.)

Figure 7.

(a) Change in time of water and oil saturation, (b) specific interfacial area between oil and water. First and second stage are defined before and after breakthrough (BT), respectively. (Online version in colour.)

Figure 8.

(a) Average mean curvature of the oil–water interface, (b) capillary pressure, before (dashed red line, 1st stage) and after (blue crosses, 2nd stage) breakthrough (BT). (Online version in colour.)

Figure 9.

Gaussian curvature of the oil/water interface. Negative values imply high connectivity and favourable flow [57]. First and second stage are defined before and after breakthrough (BT), respectively. (Online version in colour.)

Figure 10.

Thermodynamic contact angle, computed using equation (3.1) between two subsequent time steps. The 3-points moving average (dashed line) shows the increasing trend as the displacement proceeds. (Online version in colour.)