Coordination Dynamics: A Foundation for Understanding Social Behavior

Abstract

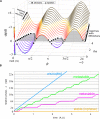
Humans' interactions with each other or with socially competent machines exhibit lawful coordination patterns at multiple levels of description. According to Coordination Dynamics, such laws specify the flow of coordination states produced by functional synergies of elements (e.g., cells, body parts, brain areas, people…) that are temporarily organized as single, coherent units. These coordinative structures or synergies may be mathematically characterized as informationally coupled self-organizing dynamical systems (Coordination Dynamics). In this paper, we start from a simple foundation, an elemental model system for social interactions, whose behavior has been captured in the Haken-Kelso-Bunz (HKB) model. We follow a tried and tested scientific method that tightly interweaves experimental neurobehavioral studies and mathematical models. We use this method to further develop a body of empirical research that advances the theory toward more generalized forms. In concordance with this interdisciplinary spirit, the present paper is written both as an overview of relevant advances and as an introduction to its mathematical underpinnings. We demonstrate HKB's evolution in the context of social coordination along several directions, with its applicability growing to increasingly complex scenarios. In particular, we show that accommodating for symmetry breaking in intrinsic dynamics and coupling, multiscale generalization and adaptation are principal evolutions. We conclude that a general framework for social coordination dynamics is on the horizon, in which models support experiments with hypothesis generation and mechanistic insights.

Keywords: Coordination Dynamics; HMI; HRI; Human Dynamic Clamp; complex systems; metastability; multiscale; social interaction.

FIGURE 1

Schematic of the experimental paradigm of social coordination dynamics in which two participants simultaneously perceive and produce behavior in view of each other. More specifically, in our canonical experiment, subjects move their fingers in continuous fashion while at the same time observing their partner doing the same. The paradigm’s simultaneity of dyadic perception and action – bidirectional coupling – is geared toward observing self-organizing processes.

FIGURE 2

Two representations of the relative phase as an order parameter connecting models and experiments. (A) shows the phase portrait of ϕ in the “extended” HKB model (Kelso et al., 1990) for various values of a diversity parameter δω. This graph carries regimes of coordination with attractors in the front of the figure (for modest diversity δω, shown; also when coupling is strong, not shown) and those without attractors (large diversity of the parts, shown in the back of the figure; and/or weak coupling, not shown). Attractors exist when the phase portrait (a function describing the rate of change of the relative phase as a function of itself) has values at $\frac{\text{d}\mathrm{\varphi }}{\text{d}t}=0$ (i.e., the coordination does not change over time) and a converging flow (filled black dots attracting the flow as indicated by the arrows). Stable regimes reflect a sustained cooperation among the system’s parts, but this stability also leads to inflexibility (see Kelso and Tognoli, 2007 for more details). In (B), four sample (unwrapped) relative phase evolutions over time illustrate stable coordination (yellow) where the order parameter ϕ persists at the same value (ad infinitum in models); metastability (magenta, green) with their characteristic dwells (quasi horizontal epochs, attracting tendencies near inphase, i.e., 0 rad. and antiphase, i.e., π rad. modulo 2π) and escape (wrapping); and uncoupled behavior (blue), whose relative phase grows continually with time (it approaches a linear function when the probability distribution of individual phases lacks remarkable joint phase ratios).

FIGURE 3

Behavioral coordination in human dyads (A), human interaction with a Human Dynamic Clamp (B), ensemble of people (C) and to hint at generality, in fireflies flashing [white circles, (D) the thick brown trace indicates the collective behavior of their large colony]. Relative phase trajectories from (A–C) are chosen to illustrate an alternation of dwells and escapes that is typical of metastability. Attracting tendencies are found toward inphase and antiphase [see histograms in (A–C), with count identified with the symbol #, showing relative phase distribution for the most strongly coupled conditions in their respective paradigms, see original references for details and for examples of weaker organization].

FIGURE 4

Augmentations of the HKB model toward increasing life-like relevance. (1) The first equation is spelled out at the oscillator level on the left (specifying the position, velocity and acceleration of oscillators x and y, with notable parameter Ω carrying the intrinsic frequency, see “Introduction” for motivation); and at a collective level on the right (specifying the rate of change of x and y’s relative phase ϕ. The coupling strength parameters a and b are responsible for the bistability of inphase and antiphase. (2) A symmetry breaking term δω (Kelso et al., 1990) gives rise to metastability. (3) A modification to the oscillators’ dynamics supplies regimes with discrete behavior -excursion from rest- and continuous cyclical behavior in a single formalism (Jirsa and Kelso, 2005), whose topology is controlled by three parameters ρ, θ, and τ. Transitions between regimes are autonomously followed in a human-machine interaction (Dumas et al., 2014). (4) The intrinsic dynamics of the oscillators Ω is coupled with adaptation rate ϵ for partners to adapt their more stable behavioral dispositions as they interact (Nordham et al., 2018). (5) A bias parameter Ψ is introduced to direct the coordination to pull human-machine dyads away from their spontaneous attractors with strength c (Dumas et al., 2014). (6) A scalable multiagent system of equations is built upon empirical data (Zhang et al., 2019) that carries the first and second order coupling term just like the original HKB model from eq. 1, under coupling matrices a and b. See references in text.