A study of the nonlinear dynamics of human behavior and its digital hardware implementation

Abstract

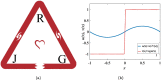
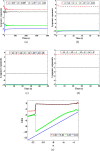
This paper introduces an intensive discussion for the dynamical model of the love triangle in both integer and fractional-order domains. Three different types of nonlinearities soft, hard, and mixed between soft and hard, are used in this study. MATLAB numerical simulations for the different three categories are presented. Also, a discussion for how the kind of personalities affects the behavior of chaotic attractors is introduced. This paper suggests some explanations for the complex love relationships depending on the impact of memory (IoM) principle. Lyapunov exponents, Kaplan-Yorke dimension, and bifurcation diagrams for three different integer-order cases show a significant dependency on system parameters. Hardware digital realization of the system is done using the Xilinx Artix-7 XC7A100T FPGA kit. Version 14.7 from the Xilinx ISE platform is used in both Verilog simulation and hardware implementation stages. The digital approach of such a system opens the door to predict the love relation after sensing the human personality. Also, this study will help in justifying more human emotions like happiness, panic, and fear accurately. Perhaps shortly, this study may combine with artificial intelligence to demonstrate Human-Computer interaction products.

Keywords: Chaos; Chaotic systems; Field programmable gate arrays; Fractional-order systems; Grünwald-Letnikov (GL); Human behavior; Love dynamics; Lyapunov exponents.

Graphical abstract

Fig. 1

Objectives of the paper.

Fig. 2

(a) Love Triangle between Romeo (R), Juliet (J) and Guinevere (G) (b) Soft and Hard nonlinearities.

Fig. 3

(a) and (b) Bifurcation diagrams for integer soft case while (a) parameter c at $(a,b,d,e,f,h)=(-3,4,2,2,-1,2^{-10})$ (b) parameter f at $(a,b,c,d,e,h)=(-3,4,-7,2,2,2^{-10})$. Figures (c) and (d) for integer hard case for parameter a at $(b,c,d,e,f,h)$ (c) $(10,-5,3,1,-5,2^{-3})$ (d) $(10,-5,3,1,-5,2^{-4})$.

Fig. 4

Lyapunov exponents for (a) soft integer nonlinearities at $(a,b,c,d,e,f$) = (−3,4,−7,2,2,−1) (b) mixed integer nonlinearities at $(a,b,c,d,e,f$) = (−10,20,−5,3,0.5,−1) (c) and (d) for hard nonlinearities with $(a,b,c,d,e,f$) = (−10,10,−5,3,1,−5) and (−5,10,−5,2,1,−1), respectively. (e) Lyapunov exponents variations with parameter a in integer soft model of the love triangle.

Fig. 5

(a) Main block diagram that used to calculate both integer-order and fractional-order cases with different nonlinearities. (b), (c) General block diagram for human love behavior with soft nonlinearity (d), (e) General block diagram for human love behavior during Hard nonlinearity using signum function.

Fig. 6

Experimental setup represented in (a). Different cases are tested with parameters (a, b, c, d, e, f ,h) values equal to (b) (−3,4,−7,2,2,−1,$2^{-10}$), (c) (−3,4,−8,2,2,−1,$2^{-10}$) for soft integer nonlinearity. Cases (d) and (e) for integer mixed nonlinearity with parameters = (−10,20,−5,3,0.5,−1,$2^{-6}$) and (−15,20,−5,3,0.5,−1,$2^{-6}$) respectively. Case (f) shows fractional-order mixed attractor with parameters (−3,1,−3,1,1.5,−1,$2^{-6}$).