Multidimensional scaling locus of memristor and fractional order elements

Abstract

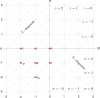
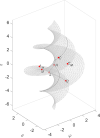
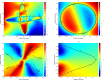
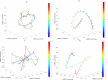
This paper combines the synergies of three mathematical and computational generalizations. The concepts of fractional calculus, memristor and information visualization extend the classical ideas of integro-differential calculus, electrical elements and data representation, respectively. The study embeds these notions in a common framework, with the objective of organizing and describing the "continuum" of fractional order elements (FOE). Each FOE is characterized by its behavior, either in the time or in the frequency domains, and the differences between the FOE are captured by a variety of distinct indices, such as the Arccosine, Canberra, Jaccard and Sørensen distances. The dissimilarity information is processed by the multidimensional scaling (MDS) computational algorithm to unravel possible clusters and to allow a direct pattern visualization. The MDS yields 3-dimensional loci organized according to the FOE characteristics both for linear and nonlinear elements. The new representation generalizes the standard Cartesian 2-dimensional periodic table of elements.

Keywords: Fractional calculus; Information visualization; Memristor; Multidimensional scaling; Procrustes analysis.

Graphical abstract

Fig. 1

Simplified Cartesian representation of the PTE of two-terminal IOE. The acronyms stand for resistor, inductor, frequency dependent negative conductance, capacitor, memristor, meminductor, memcapacitor.

Fig. 2

The 3-dimensional representation of the PTE of two-terminal IOE using the coordinate transformation (16). The acronyms $\{R,L,D,C,M,L_M,C_M\}$ stand for $\{$resistor, inductor, frequency dependent negative conductance, capacitor, memristor, meminductor, memcapacitor$\}$.

Fig. 3

Block diagram of a FOE where $\psi (·)$ is some linear/nonlinear function: input $i\left(t\right)$ and output $v\left(t\right)$ given by $x_{d,e}\left(t\right)=A_e\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{d}t\right)$ and $z_{d,e}\left(t\right)=\psi \left[A_e{\omega }_d^{{\gamma }_n}\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{d}t+{\gamma }_n\frac{\pi }{2}\right)\right]$, respectively.

Fig. 4

The 3-dimensional loci of $N=721$ linear FOE, characterized in the time domain by means of the distances: (a) ${\delta }_A$; (b) ${\delta }_C$; (c) ${\delta }_J$; (d) ${\delta }_S$. The markers represent the FOE and their color varies with the FOE order ${\gamma }_n\in [-10,10]$. The other parameters are $N_{\omega }=40$, ${\omega }_d\in [10^{-1},10^1]$, $N_A=1$, $N_t=1000$ and $N_p=5$. In the loci (a) and (b) the IOE of the same category are connected with dashed lines.

Fig. 5

The 2 + 1-dimensional loci of $N=721$ linear FOE, characterized in the time domain by means of the distances: (a) ${\delta }_A$; (b) ${\delta }_C$; (c) ${\delta }_J$; (d) ${\delta }_S$. The $z$ coordinate of the loci is calculated by means of RBI based on the value of ${\gamma }_n\in [-10,10]$ at each MDS $(x,y)$ coordinate. The other parameters are $N_{\omega }=40$, ${\omega }_d\in [10^{-1},10^1]$, $N_A=1$, $N_t=1000$ and.$N_p=5$

Fig. 6

The 3-dimensional loci of $N=721$ linear FOE, characterized in the frequency domain by means of the distances: (a) ${\delta }_A$; (b) ${\delta }_C$; (c) ${\delta }_J$; (d) ${\delta }_S$. The markers represent the FOE and their color varies with the FOE order ${\gamma }_n\in [-10,10]$. The other parameters are $N_{\omega }=40$, ${\omega }_d\in [10^{-1},10^1]$, $N_A=1$, $N_t=1000$ and $N_p=5$. In the loci (a) and (b) the IOE of the same category are connected with dashed lines.

Fig. 7

The 3-dimensional loci of $N=721$ nonlinear ($\psi$ of degree 3) FOE, characterized in the time domain by means of the distances: (a) ${\delta }_A$; (b) ${\delta }_C$; (c) ${\delta }_J$; (d) ${\delta }_S$. The markers represent the FOE and their color varies with the FOE order ${\gamma }_n\in [-10,10]$. The other parameters are $N_{\omega }=40$, ${\omega }_d\in [10^{-1},10^1]$, $N_A=10$, $N_e\in [10^{-2},10^2]$, $N_t=1000$ and $N_p=5$. In the loci (a) and (c) the IOE of the same category are connected with dashed lines.

Fig. 8

The 3-dimensional loci of $N=721$ nonlinear ($\psi$ of degree 3) FOE, characterized in the frequency domain by means of the distances: (a) ${\delta }_A$; (b) ${\delta }_C$; (c) ${\delta }_J$; (d) ${\delta }_S$. The markers represent the FOE and their color varies with the FOE order $\gamma \in [-10,10]$. The other parameters are $N_{\omega }=40$, ${\omega }_d\in [10^{-1},10^1]$, $N_A=10$, $N_e\in [10^{-2},10^2]$, $N_t=1000$ and $N_p=5$. In the loci (a) and (d) the IOE of the same category are connected with dashed lines.

Fig. 9

Three superimposed 3-dimensional loci of $N=721$ FOE (using Procrustes), characterized in the time domain by means of the distances: (a) ${\delta }_A$; (b) ${\delta }_C$; (c) ${\delta }_J$; (d) ${\delta }_S$. The functions $\psi$ of degree 1 (linear case), 3 and 5 are adopted.

Fig. 10

Three superimposed 3-dimensional loci of $N=721$ FOE (using Procrustes), characterized in the frequency domain by means of the distances: (a) ${\delta }_A$; (b) ${\delta }_C$; (c) ${\delta }_J$; (d) ${\delta }_S$. The functions $\psi$ of degree 1 (linear case), 3 and 5 are adopted.