Depth-selective data analysis for time-domain fNIRS: moments vs. time windows

Abstract

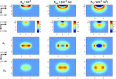
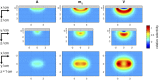
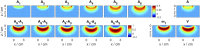
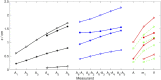
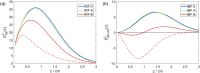
Time-domain measurements facilitate the elimination of the influence of extracerebral, systemic effects, a key problem in functional near-infrared spectroscopy (fNIRS) of the adult human brain. The analysis of measured time-of-flight distributions of photons often relies on moments or time windows. However, a systematic and quantitative characterization of the performance of these measurands is still lacking. Based on perturbation simulations for small localized absorption changes, we compared spatial sensitivity profiles and depth selectivity for moments (integral, mean time of flight and variance), photon counts in time windows and their ratios for different time windows. The influence of the instrument response function (IRF) was investigated for all measurands and for various source-detector separations. Variance exhibits the highest depth selectivity among the moments. Ratios of photon counts in different late time windows can achieve even higher selectivity. An advantage of moments is their robustness against the shape of the IRF and instrumental drifts.

Fig. 1.

Integrands and their constituents for calculation of (a) mean time of flight m₁, (b) variance V, and (c) photon counts in consecutive time windows of 500 ps width. The time-of-flight distribution N(t) represents time-resolved diffuse reflectance obtained for a semi-infinite homogeneous medium with reduced scattering coefficient μ_s′ = 10 cm^-1, absorption coefficient μ_a = 0.1 cm^-1, refractive index n = 1.4 and for source-detector separation ρ = 3 cm, based on the diffusion model and extrapolated boundary conditions [59]. N(t) and G(t)N(t) in (a,b) were normalized to their respective maxima. Poisson noise shown in (a,b) was simulated for N_tot = 10⁶ and 5 ps width of the histogram time bins.

Fig. 2.

Spatial distributions of sensitivity factors S_M related to the measurands (M) attenuation A (left column), mean time of flight m₁ (middle column), and variance V (right column) for a semi-infinite homogeneous medium with μ_s′ = 10 cm^-1, μ_a = 0.1 cm^-1, n = 1.4 (also valid for all subsequent figures) and a source-detector separation ρ = 3 cm. The positions of the point-like source and detector are (0, 0, z₀) with z₀ = 1/μ_s′ and (ρ, 0, 0), respectively. The top row shows a cut along the plane y = 0, the second row along the plane x = ρ/2 and the third and fourth rows along planes parallel to the surface, at two different depths z = z₁ = 0.5 cm and z = z₂ = 1 cm. The color scales are the same within each column. They range from -0.64 to 1.6 times the maximum sensitivity in the y-z cuts (second row), S_M,max(x = ρ/2, y, z).

Fig. 3.

Spatial distributions of depth selectivity for moments A, m₁ and V, for depths z > 0.5 cm, obtained by normalizing the 3D sensitivities plotted in Fig. 2 to the total sensitivity within the upper layer (z ≤ 0.5 cm). The third row refers to the cut at z = z₂ = 1 cm. The color scales are the same in all panels, ranging from -0.48 to 1.2 times the maximum for S_V in the y-z cut.

Fig. 4.

Comparison of sensitivity distributions (integrated over y direction) for various measurands M related to time windows and moments. Top row, panels 1-6: Attenuation A_k in consecutive time windows of equal width (500 ps) as shown in Fig. 1(c). Bottom row, panels 1-5: Attenuation difference A_l – A_e between late (l) and early (e) time windows. The selection of the early time window was varied (1 to 5) while the late window was always the last one (6^th). Right part of the figure: Related plots for moments, A (top row, panel 7), m₁ and V (bottom row, panels 6 and 7). The plot in each panel is normalized to its maximum value, the relative color bar in each row is valid for all panels in that row.

Fig. 5.

Depth-dependent sensitivities and depth selectivity for moments and time windows for different source-detector separations. (a) Comparison of sensitivities for moments at ρ = 2 cm and 3 cm. Sensitivities for each moment (A, m₁ and V) were normalized to their maxima for ρ = 3 cm. (b) Comparison of sensitivities for time-window measurands, all normalized to the maximum sensitivity for A₆. Data shown for ρ = 3 cm, sensitivities for ρ = 2 cm are very similar. (c) Depth selectivity for moments vs. depth position (upper boundary) z_L of lower layer, schematic shown in the inset. (d) Depth selectivity for time-window measurands.

Fig. 6.

Characteristics of the z-dependent sensitivities for all measurands, comparing the positions of their maxima (*), FWHM (▪) and z positions at 50% of maximum sensitivity toward smaller ($⊲$) and larger ($⊳$) z values. Parameters for time-window measurands were calculated for ρ = 3 cm (valid for 2 cm as well). Results for moments are provided for ρ = 2 cm (green dashed lines) and ρ = 3 cm (red solid lines).

Fig. 7.

Examples of two IRFs: (a) IRF A, (b) IRF B (see text for details), together with simulated (unperturbed) DTOFs for ρ = 2 cm and ρ = 3 cm before (dashed lines) and after (solid lines) convolution with the IRF. The 6^th time window is marked by a yellow rectangle.

Fig. 8.

2D sensitivity plots for the time-window measurands (analogous to Fig. 4), normalized to maximum in each panel, for IRF B, (a) for ρ = 2 cm and (b) for ρ = 3 cm.

Fig. 9.

Depth-dependent sensitivities S_M^L(z) (a) for A₆ and (b) for A₆ – A₅, for ρ = 2 cm (dashed lines) and ρ = 3 cm (solid lines). IRF 0 denotes a Dirac delta-pulse like IRF.

Fig. 10.

Contrast, noise and their ratio as a function of the upper integration limit t_up for A, m₁ and V (columns of panels) at ρ = 2 cm for an absorption change of Δµ_a = 0.001 cm^-1 in a layer extending from z = 1.05 cm to z = 1.5 cm and for the instrument response functions IRF 0 (blue), IRF A (green) and IRF B (red), illustrated in Fig. 7. (a-c) Contrast (top row of panels), (d-f) Noise (standard deviation due to Poisson noise) (middle row), (g-i) Contrast-to-noise ratio (bottom row).