Accurate determination of node and arc multiplicities in de bruijn graphs using conditional random fields

Abstract

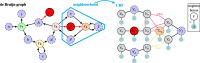
Background: De Bruijn graphs are key data structures for the analysis of next-generation sequencing data. They efficiently represent the overlap between reads and hence, also the underlying genome sequence. However, sequencing errors and repeated subsequences render the identification of the true underlying sequence difficult. A key step in this process is the inference of the multiplicities of nodes and arcs in the graph. These multiplicities correspond to the number of times each k-mer (resp. k+1-mer) implied by a node (resp. arc) is present in the genomic sequence. Determining multiplicities thus reveals the repeat structure and presence of sequencing errors. Multiplicities of nodes/arcs in the de Bruijn graph are reflected in their coverage, however, coverage variability and coverage biases render their determination ambiguous. Current methods to determine node/arc multiplicities base their decisions solely on the information in nodes and arcs individually, under-utilising the information present in the sequencing data.

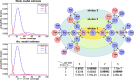
Results: To improve the accuracy with which node and arc multiplicities in a de Bruijn graph are inferred, we developed a conditional random field (CRF) model to efficiently combine the coverage information within each node/arc individually with the information of surrounding nodes and arcs. Multiplicities are thus collectively assigned in a more consistent manner.

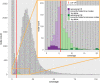
Conclusions: We demonstrate that the CRF model yields significant improvements in accuracy and a more robust expectation-maximisation parameter estimation. True k-mers can be distinguished from erroneous k-mers with a higher F₁ score than existing methods. A C++11 implementation is available at https://github.com/biointec/detox under the GNU AGPL v3.0 license.

Keywords: De Bruijn graphs; Next-generation sequencing; Probabilistic graphical models.

Fig. 1

Illustration of the issues when assigning multiplicities based only on a k-mer histogram based cutoff. a A k-mer histogram that consists of a mixture of negative binomial distributions. Each component models the k-mer coverage variability for a particular multiplicity. The two-sided arrows delineate the coverage intervals corresponding to a multiplicity estimate. Note how large areas under the curve of a particular multiplicity fall in an interval of a different estimated multiplicity. b Example genome sequence with corresponding reads and de Bruijn graph. Nodes and arcs are labelled with their read coverage. Nodes are also labelled with their corresponding fragment in the genome sequence. Sequencing errors cause spurious nodes and arcs in the de Bruijn graph, such as node e^′ and j. Nodes are encircled according to their true multiplicity (cf. the patterns in Fig. 1a), all correct arcs have true multiplicity 1. c Most likely multiplicity assignment to nodes and arcs based on the k-mer histogram in Fig. 1a. This assignment leads to inconsistencies: nodes where there is a conservation of flow of multiplicity are marked with ✓, nodes where this is violated are marked with ✗. d Multiplicity assignment such that conservation of flow of multiplicity holds in each node. These assignments are correct for all nodes and arcs and reveal sequencing errors (nodes/arcs with multiplicity zero) and the repeat structure of the genome sequence

Fig. 2

De Bruijn graph of Fig. 1b. In the de Bruijn graph a neighbourhood of size 1 around node r₄ was selected and the CRF corresponding to this neighbourhood is shown. Nodes Y_n in the CRF correspond to nodes n in the de Bruijn graph, while the Y_a-nodes correspond to the arcs in the de Bruijn graph. Here, each node Y is connected to a node X by an edge arising from a singleton factor φ which contains the information about the coverage of that node or arc in the de Bruijn graph. Note, however, that a node that contains fewer than 2kk-mers will not have such corresponding X and factor φ. All connections between Y-nodes arise from conservation of flow factors. The two cliques arising from the flow through r₄ are shown explicitly

Fig. 3

Subgraph of the de Bruijn graph built from the real P. aeruginosa dataset (30×). Nodes and arcs are labelled with their (average) coverage. The fitted node and arc models are shown on the left. The nodes of the graph are coloured according to their true multiplicity. The neighbourhoods of size 1, 2 and 3 surrounding node n₁ are shown as coloured ellipses. The inset table shows the categorical distribution $P\left(Y_{n_1}\right)$ of the multiplicities {0,1,2} for node n₁ for different neighbourhood sizes. For small neighbourhoods (sizes 0 and 1), node n₁ (incorrectly) appears to represent a sequencing error due to its relatively low coverage. At neighbourhood sizes 2 and 3, the CRF model has enough information to (correctly) infer multiplicity 1 for node n₁ with high probability

Fig. 4

Part of the q-mer histogram of the real P. aeruginosa (25×) dataset. The red line shows the optimal coverage cutoff value. The purple shaded area represents nodes with a coverage below this cutoff value that have true multiplicity 1 whereas the green shaded area represents nodes with a coverage above the cutoff that have true multiplicity 0. These nodes represent false positives and false negatives respectively when using a cutoff-based method. In contrast, the CRF model is able to correctly classify the majority of nodes (lighter shaded purple and green areas)