New insights and best practices for the successful use of Empirical Mode Decomposition, Iterative Filtering and derived algorithms
- PMID: 32939024
- PMCID: PMC7495475
- DOI: 10.1038/s41598-020-72193-2
New insights and best practices for the successful use of Empirical Mode Decomposition, Iterative Filtering and derived algorithms
Abstract
Algorithms based on Empirical Mode Decomposition (EMD) and Iterative Filtering (IF) are largely implemented for representing a signal as superposition of simpler well-behaved components called Intrinsic Mode Functions (IMFs). Although they are more suitable than traditional methods for the analysis of nonlinear and nonstationary signals, they could be easily misused if their known limitations, together with the assumptions they rely on, are not carefully considered. In this work, we examine the main pitfalls and provide caveats for the proper use of the EMD- and IF-based algorithms. Specifically, we address the problems related to boundary errors, to the presence of spikes or jumps in the signal and to the decomposition of highly-stochastic signals. The consequences of an improper usage of these techniques are discussed and clarified also by analysing real data and performing numerical simulations. Finally, we provide the reader with the best practices to maximize the quality and meaningfulness of the decomposition produced by these techniques. In particular, a technique for the extension of signal to reduce the boundary effects is proposed; a careful handling of spikes and jumps in the signal is suggested; the concept of multi-scale statistical analysis is presented to treat highly stochastic signals.
Conflict of interest statement
The authors declare no competing interests.
Figures

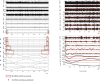



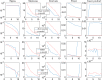
References
-
- Bracewell R. N, Bracewell R. N. The Fourier transform and its applications. New York: McGraw-Hill; 1986.
-
- Cicone, A. Nonstationary signal decomposition for dummies. in Advances in Mathematical Methods and High Performance Computing 69–82 (Springer, New York, 2019).
-
- Cohen L. Time-frequency analysis. New York: Prentice hall; 1995.
-
- Daubechies I, Lu J, Wu HT. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmonic Anal. 2011;30:243–261. doi: 10.1016/j.acha.2010.08.002. - DOI
-
- Auger F, et al. Time-frequency reassignment and synchrosqueezing: An overview. IEEE Signal Process. Mag. 2013;30:32–41. doi: 10.1109/MSP.2013.2265316. - DOI
LinkOut - more resources
Full Text Sources
Miscellaneous

