Differential tissue stiffness of body column facilitates locomotion of Hydra on solid substrates
- PMID: 32958523
- PMCID: PMC7116704
- DOI: 10.1242/jeb.232702
Differential tissue stiffness of body column facilitates locomotion of Hydra on solid substrates
Abstract
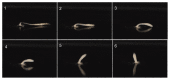
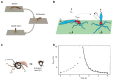
The bell-shaped members of the Cnidaria typically move around by swimming, whereas the Hydra polyp can perform locomotion on solid substrates in an aquatic environment. To address the biomechanics of locomotion on rigid substrates, we studied the 'somersaulting' locomotion in Hydra We applied atomic force microscopy to measure the local mechanical properties of Hydra's body column and identified the existence of differential Young's modulus between the shoulder region versus rest of the body column at 3:1 ratio. We show that somersaulting primarily depends on differential tissue stiffness of the body column and is explained by computational models that accurately recapitulate the mechanics involved in this process. We demonstrate that perturbation of the observed stiffness variation in the body column by modulating the extracellular matrix polymerization impairs the 'somersault' movement. These results provide a mechanistic basis for the evolutionary significance of differential extracellular matrix properties and tissue stiffness.
Keywords: Atomic force microscopy; Biomechanics; Extracellular matrix; Tissue rheology.
© 2020. Published by The Company of Biologists Ltd.
Conflict of interest statement
Competing interestsThe authors declare no competing or financial interests.
Figures





Similar articles
-
Alteration of Young's modulus in mesenchymal stromal cells during osteogenesis measured by atomic force microscopy.Biochem Biophys Res Commun. 2020 Jun 4;526(3):827-832. doi: 10.1016/j.bbrc.2020.03.146. Epub 2020 Apr 6. Biochem Biophys Res Commun. 2020. PMID: 32273088
-
Measured pulmonary arterial tissue stiffness is highly sensitive to AFM indenter dimensions.J Mech Behav Biomed Mater. 2017 Oct;74:118-127. doi: 10.1016/j.jmbbm.2017.05.039. Epub 2017 May 31. J Mech Behav Biomed Mater. 2017. PMID: 28595103 Free PMC article.
-
Effect of substrate stiffness on the mechanical properties of cervical cancer cells.Arch Biochem Biophys. 2022 Aug 15;725:109281. doi: 10.1016/j.abb.2022.109281. Epub 2022 May 7. Arch Biochem Biophys. 2022. PMID: 35537506
-
Components, structure, biogenesis and function of the Hydra extracellular matrix in regeneration, pattern formation and cell differentiation.Int J Dev Biol. 2012;56(6-8):567-76. doi: 10.1387/ijdb.113445ms. Int J Dev Biol. 2012. PMID: 22689358 Review.
-
Cell stiffness determined by atomic force microscopy and its correlation with cell motility.Biochim Biophys Acta. 2016 Sep;1860(9):1953-60. doi: 10.1016/j.bbagen.2016.06.010. Epub 2016 Jun 8. Biochim Biophys Acta. 2016. PMID: 27288584 Review.
Cited by
-
A complete biomechanical model of Hydra contractile behaviors, from neural drive to muscle to movement.Proc Natl Acad Sci U S A. 2023 Mar 14;120(11):e2210439120. doi: 10.1073/pnas.2210439120. Epub 2023 Mar 10. Proc Natl Acad Sci U S A. 2023. PMID: 36897982 Free PMC article.
-
Phototaxis is a satiety-dependent behavioral sequence in Hydra vulgaris.J Exp Biol. 2024 Sep 15;227(18):jeb247503. doi: 10.1242/jeb.247503. Epub 2024 Sep 25. J Exp Biol. 2024. PMID: 39155640 Free PMC article.
-
Mechanical characterization of regenerating Hydra tissue spheres.Biophys J. 2024 Jul 2;123(13):1792-1803. doi: 10.1016/j.bpj.2024.05.022. Epub 2024 May 23. Biophys J. 2024. PMID: 38783602 Free PMC article.
-
A soft microrobot with highly deformable 3D actuators for climbing and transitioning complex surfaces.Proc Natl Acad Sci U S A. 2022 Dec 6;119(49):e2215028119. doi: 10.1073/pnas.2215028119. Epub 2022 Nov 28. Proc Natl Acad Sci U S A. 2022. PMID: 36442122 Free PMC article.
References
-
- Alexander RM. Principles of Animal Locomotion. Princeton University Press; 2003.
-
- Anderson EJ, Demont ME. The mechanics of locomotion in the squid Loligo pealei: locomotory function and unsteady hydrodynamics of the jet and intramantle pressure. J Exp Biol. 2000;203:2851–2863. - PubMed
Publication types
MeSH terms
Associated data
Grants and funding
LinkOut - more resources
Full Text Sources

